【エンジン】吸気流量を得るための仕様化 【エアフロメータ】

はじめに

※ 本記事の以下を親記事とした子記事に位置付けられる。
https://www.simulationroom999.com/blog/physical-value-conversion/

前回までにエアフロメータから吸気流量を求める関数を導出した。
これを実際のECUに組み込む際の仕様に落とし込む必要がある。
今回はSimulinkモデル風に仕様表現してみる。

実際に積分を考える際は $\sum$ ではなく、「移動平均」を保持している方が有利であることが多い。
「 $2 T D C$ 間の移動平均」が分かっており、後は「 $2 T D C$ 時間」が分かれば、

$\int M_{a i r} [g / s e c] d t [s e c] = 2 T D C 間の移動平均 [g / s e c] \times 2 T D C 時間 [s e c]$

となり、結果として

$G_{a i r} [g] = 2 T D C 間の移動平均 [g / s e c] \times 2 T D C 時間 [s e c]$

となる。

移動平均と時間積分はかなり密接な関係にあると言って良い。
(ノイズ除去用フィルタだと思ってたら大間違いってことは多い。)

とりあえず、何も考えずにモデル化すると以下となる。

※ 吸気流量とエンジン回転数の関係性については以下の記事で記載。

処理タイミングとしては、以下2つ。

考えられ改善点としては以下。

論理モデルは数式をそのまま表現したものであったが、実装モデルの段階では処理負荷を考え演算を最適化したり、処理周期が長い方に演算を寄せたりする。
今回の場合だと以下のようになる。

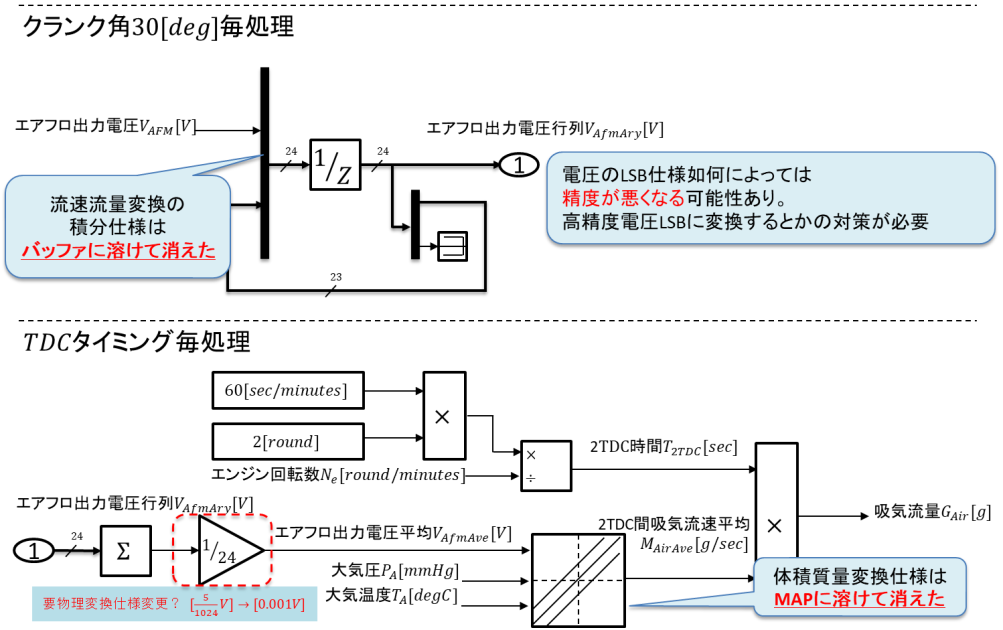
かなりスッキリした状態になる。
一見すると消えた仕様があるが、消えたというよりも別の概念に溶けたイメージ。

このように実装モデルだけ見ると、元の数式が分からなくなることが多い。
よって、仕様のトレーサビリティが重要という話が良く現場では出てくる。