【入門】重要な極限値【数値計算】

はさみうちの原理
sinc関数
まとめ

はさみうちの原理

はさみうちの原理についてはWikipediaを引用しよう。

はさみうちの原理（はさみうちのげんり）は、極限に関する定理の一つ。おおまかには、同じ極限値を持つ2つの関数に挟まれた第3の関数も同じ極限値を持つという主張である。
Wikipediaより(https://ja.wikipedia.org/wiki/%E3%81%AF%E3%81%95%E3%81%BF%E3%81%86%E3%81%A1%E3%81%AE%E5%8E%9F%E7%90%86)

これ見てもよく分からないかもしれないが、
ポイントは、以下の式になる。

\(
\displaystyle 1 > \frac{\sin(x)}{x} > \cos(x)
\)

ここで、\(\cos(0)\)は\(1\)になる。
よって、\(\frac{\sin(x)}{x}\)も\(1\)に収束しないと辻褄が合わない。
という理屈になる。

sinc関数

今回扱った、\(\displaystyle\frac{\sin}{x}\)は
通称sinc関数と呼ばれるもの。

こういう名前が付いているってことは割と重要な関数ってことになると思ってOK。

今回のフーリエ係数にとっても重要なのだが、
ディジタル信号処理に於いても重要な関数のようである。
今回はそこには触れないが、
どのような波形になるかは確認しておこう。
(数式だけじゃもよくわからんだろうし。)

MATLABコードで書くと以下になる。

sinc = @(x) sin(x)./x
x=-50:0.01:50
plot(x,sinc(x))
grid

そして処理結果

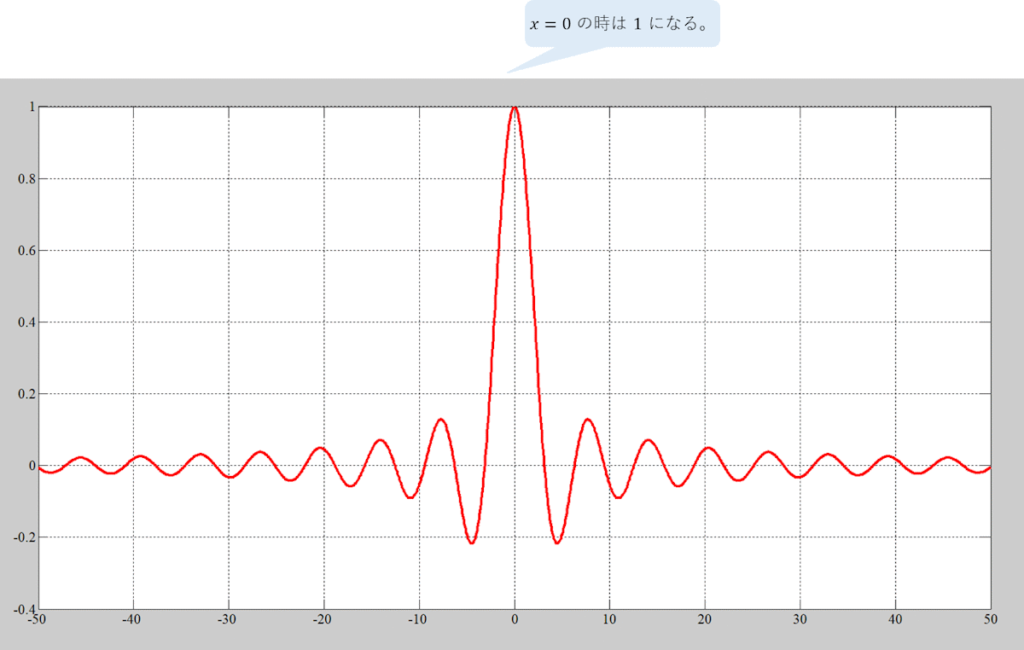
xが0の時は1になってる。

実際は、MATLABで演算した場合、sin(0)/0はNaNになるのだが、
0近辺が1に限りなく近いことはわかるだろう。
ちなみにPythonだと以下のコードになる。

import numpy as np
import matplotlib.pyplot as plt

def sinc(x):
    return np.sin(x)/x  

x = np.arange(-50, 50, 0.01)
plt.plot(x, sinc(x))
plt.grid(True)
plt.show()