プログラムの流れ
作成するプログラムのフローは以下となる。
- 目的関数の定義
- 目的関数の導関数の定義
- 入力初期値設定
- ハイパーパラメータの設定
- 勾配降下法の実装
- 結果表示
- グラフへのプロット
「目的関数の定義」と「目的関数の導関数の定義」は
先ほどの関数とその導関数の話になる。
「入力初期値」、「ハイパーパラメータ」は少し説明が必要かもしれない。
「結果表示」は学習結果。
グラフへのプロットもそのままではあるが、
ある程度の学習過程が分かるようなプロット方法で実装する予定。
入力初期値設定
まずは、入力初期値設定だが、
これは単純に2.9にしておく。
先ほど見せたグラフをべースにするとこの位置を入力初期値とする。
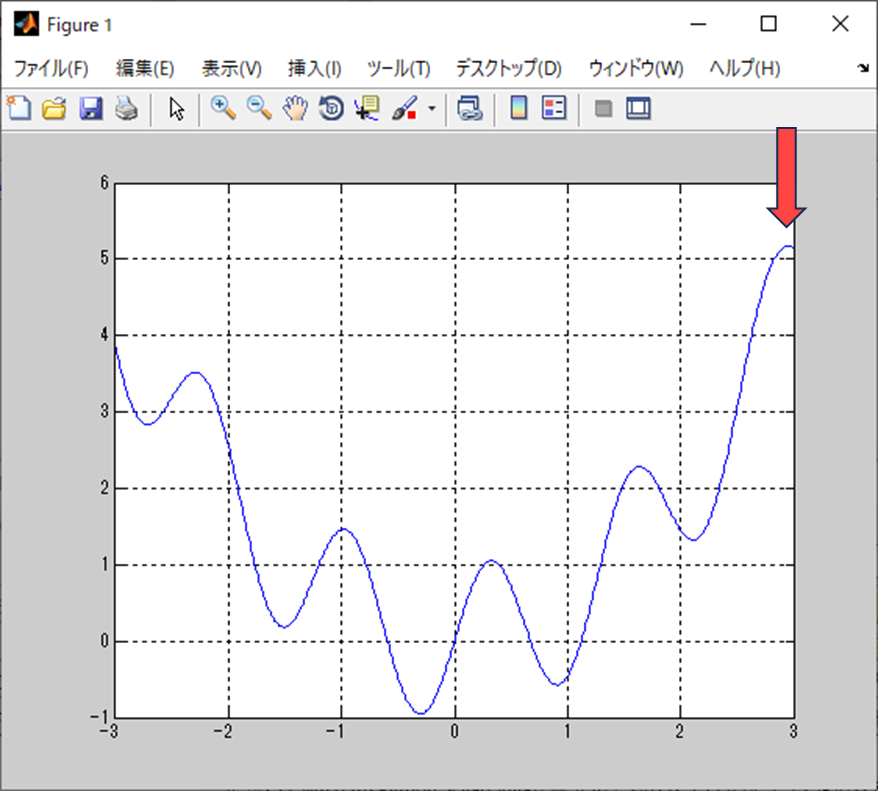
上の方から下っていく感じを想定している。
名前の通り、勾配を降下している様子が見れると思う。
ハイパーパラメータの設定
次はパイパーパラメータ
パイパーパラメータは、モデルが学習する上での設定値だと思えばOK。
ただし、最適化アルゴリズム毎に変わるところではある。
とりあえず、今回のハイパーパラメータだけを提示する。
- 学習率
- 勾配大きさに対して重みを変動させる係数
- 最大イテレーション数
- 勾配降下法の実行回数
と言う感じで学習時の設定値というのがわかるだろう。
グラフへのプロット
グラフへのプロットだが、
学習の経緯も見れた方が良い。
というわけで、学習過程の入力の軌跡や誤差の動きを記録する。
勾配降下法を実施する際にfor分で回すことになるので、
それぞれの変数を配列として保存して、あとでグラフで表示するという感じになる。
具体的な実装は、これから作るソースコードを見てもらった方が良いだろう。
プログラムの振る舞いの雰囲気
実際のプログラムの振る舞いを事前に出しておこう。
分かり易いようにアニメーションgifにしてある。
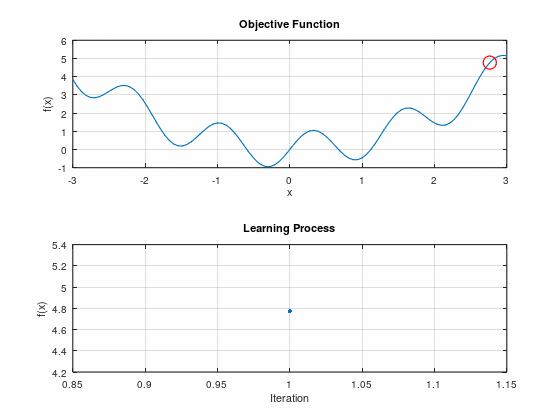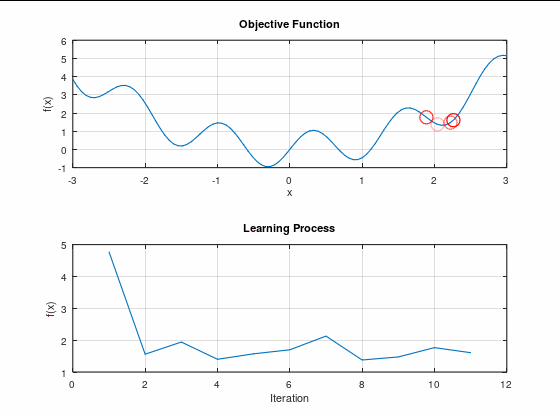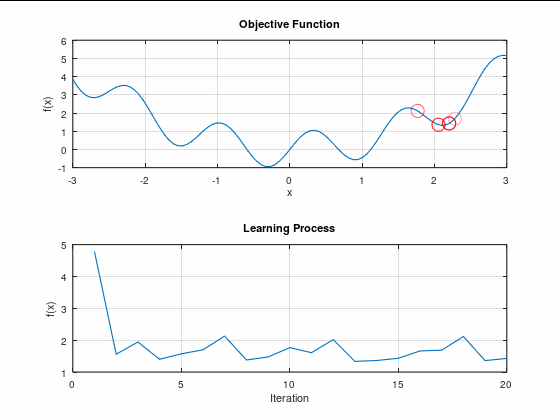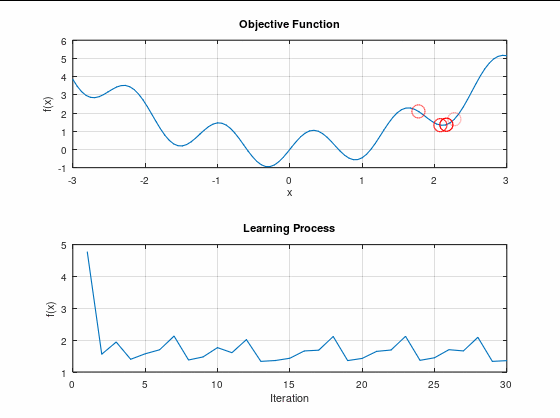
ごちゃごちゃ動いてはいるが、最小値までは到達できていない。
こういう状況を「局所最適解に陥る」と言ったりする。
最適解は共に誤差関数の極小値ではあるのだが、最小値ではない。
最小値ではない極小値が局所最適解。
最小値な極小値が大域最適解。
と呼ばれている。
これが勾配降下法の問題。
それ以外にも様々な問題はあるのだが、
直近でぶち当たる問題がこれになる。
まとめ
- 勾配降下法に概念レベルの説明。
- 勾配降下法をプログラム的に確認する方法としてニューラルネットワークではなく、任意の関数に試す方法がある。
- 勾配降下法プログラムのフローで分かりにくいところを説明。
MATLAB、Python、Scilab、Julia比較ページはこちら
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント