【入門】勾配降下法(Python)【数値計算】

ATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
【再掲】勾配降下法の確認プログラムのフロー
Pythonコード
処理結果
考察
まとめ

はじめに

の、

MATLAB,Python,Scilab,Julia比較第4章その47【勾配降下法⑤】

を書き直したもの。

勾配降下法をプログラム的に確認する。
今回はPython。

【再掲】勾配降下法の確認プログラムのフロー

とりあえず、勾配降下法の確認プログラムのフローを再掲

目的関数の定義
目的関数の導関数の定義
入力初期値設定
ハイパーパラメータの設定
勾配降下法の実装
結果表示
グラフへのプロット

これをPythonで実施する。

Pythonコード

Pythonコードは以下。

import numpy as np
import matplotlib.pyplot as plt

# 目的関数の定義（例: f(x) = sin(5x) + 0.5x^2）
def f(x):
    return np.sin(5*x) + 0.5*x**2

# 目的関数の微分（例: df(x)/dx = 5cos(5x) + x）
def df(x):
    return 5*np.cos(5*x) + x

# 初期値の設定
x = 2.9  # 初期値

# ハイパーパラメータの設定
learning_rate = 0.1  # 学習率
max_iterations = 100  # 最大イテレーション数

# 学習過程を保存するための変数
x_history = np.zeros(max_iterations)
f_history = np.zeros(max_iterations)

# 勾配降下法の実装
for i in range(max_iterations):
    # 勾配の計算
    gradient = df(x)

    # パラメータの更新
    x = x - learning_rate * gradient

    # 学習過程の保存
    x_history[i] = x
    f_history[i] = f(x)

# 結果の表示
print('optimal solution:')
print(x)
print('optimal value:')
print(f(x))

# グラフのプロット
fig, axes = plt.subplots(2, 1)

# Objective Functionのプロット
x_vals = np.linspace(-3, 3, 100)
f_vals = f(x_vals)
axes[0].plot(x_vals, f_vals)
axes[0].scatter(x_history, f_history, color='r')
axes[0].set_xlabel('x')
axes[0].set_ylabel('f(x)')
axes[0].set_title('Objective Function')
axes[0].grid()

# Learning Processのプロット
iterations = np.arange(1, max_iterations + 1)
axes[1].plot(iterations, f_history)
axes[1].set_xlabel('Iteration')
axes[1].set_ylabel('f(x)')
axes[1].set_title('Learning Process')
axes[1].grid()

plt.tight_layout()
plt.show()

処理結果

処理結果は以下。

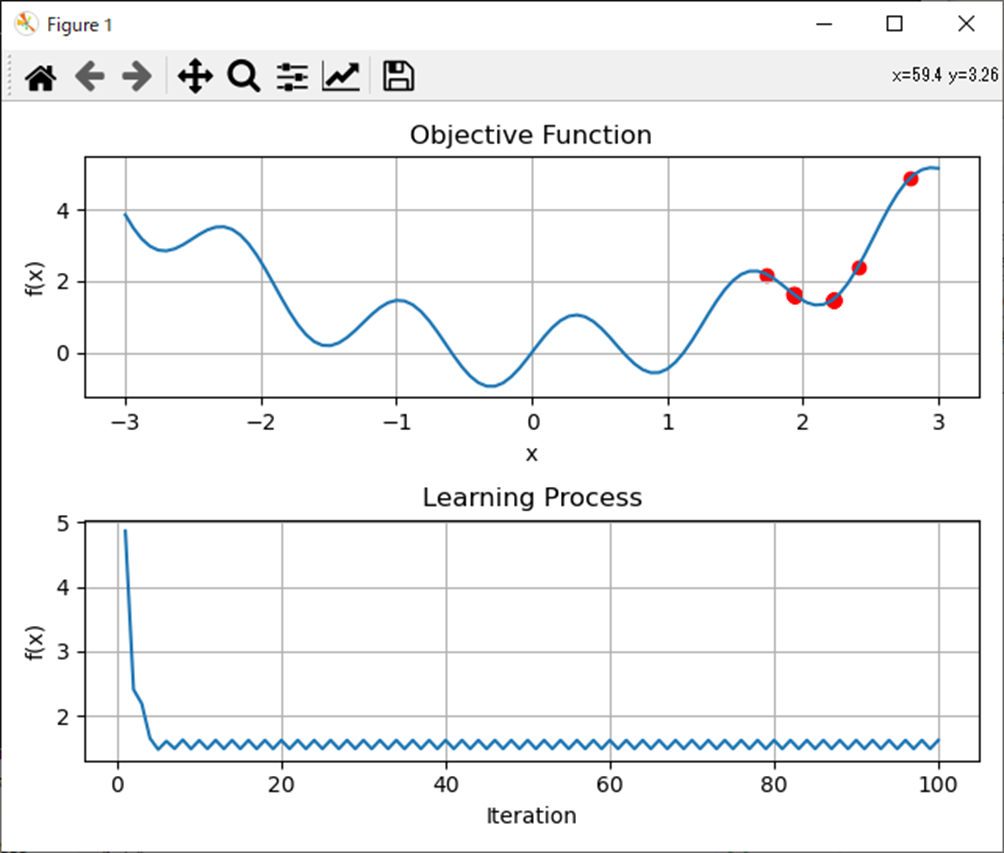
optimal solution:
1.936047911053309
optimal value:
1.6214487071489236

考察

MATLABと同じ結果で、局所最適解に陥ってる。
回避方法も最適化アルゴリズムによる学習率の動的な変更になる。

まとめ

勾配降下法の実験をPythonで実施。
予想通り局所最適解に陥った。
局所最適解の回避方法としては学習率を状況に応じて変更する様々は最適化アルゴリズムがある。
- モーメンタム、AdaGrad、Adamなどなど。

MATLAB、Python、Scilab、Julia比較ページはこちら

Pythonで動かして学ぶ！あたらしい線形代数の教科書

Amazon.co.jp

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

Amazon.co.jp

ゼロからはじめるPID制御

https://amzn.to/3SvzuyR

OpenCVによる画像処理入門

https://amzn.to/498ZUgK

恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]

Amazon.co.jp

Pythonによる制御工学入門

Amazon.co.jp

理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析

https://amzn.to/3UAunQK