【入門】勾配降下法【数値計算】

はじめに

の、

MATLAB,Python,Scilab,Julia比較第4章その43【勾配降下法①】
MATLAB,Python,Scilab,Julia比較第4章その44【勾配降下法②】
MATLAB,Python,Scilab,Julia比較第4章その45【勾配降下法③】

を書き直したもの。

再び連鎖律の解説に戻る。
今回は勾配降下法関連の話

多変量関数の連鎖律の話が終わったので、
また元の連鎖律を把握するフローに戻ってくる。

残すは勾配降下法のみとなる。

まず勾配降下法の概念的な説明。
目的変数と単純パーセプトロンの差を誤差\(E\)とし、
重みを\(W\)とする。
この二つのパラメータの関係をグラフにした場合、
以下の図のようなことをしたいのが勾配降下法。

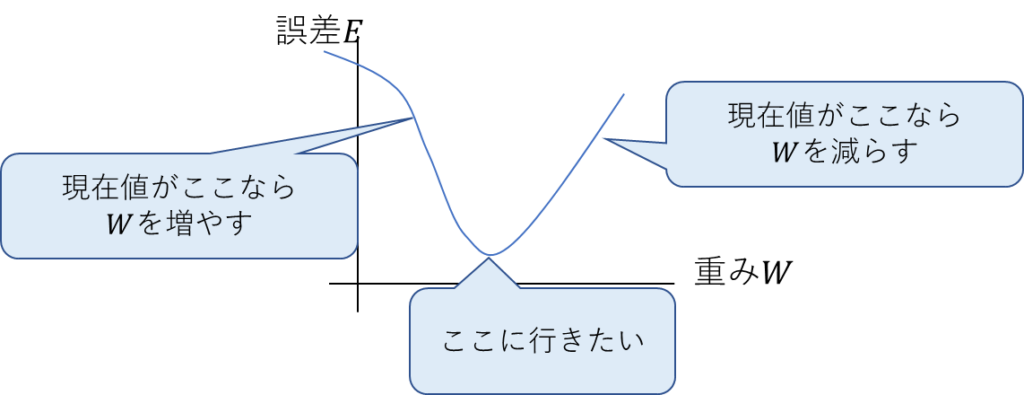
つまり、誤差を最小化したいってことになる。
しかし、どうやって最小値にたどり着くのだろう？
シンプルに考えると値を振って探すことではあるが、
それだと、以前やった総当たり法と変わらない。

勾配降下法は微分を使う。
微分は関数の傾きがわかる。
要は以下のことをすればOK。

微分すればOKと言ったが、
単純パーセプトロンもそこそこややこしい構成に成っている。
普通に考えたら微分できなそう。

そこで前回までにやった「多変量関数の連鎖律」の出番となる。
「多変量関数の連鎖律」が分かるってことは単純パーセプトロン全体の導関数が分かるってことなので、
あらゆる点に於ける微分もわかるってことになる。
厄介なシグモイド関数も導関数が分かってるので。

そこらへんの一連の流れを誤差逆伝播法と言ったりする。
実際は多層パーセプトロン以上のモデルで使う用語ではあるので、
単純パーセプトロンで使用する場合は、言い分ける都合で「逆伝播」という言い方に留めておこう。

その逆伝播ってのを早速試してみる感じになるのだが、
その前に勾配降下法のみの実験をやってみるつもり。
勾配降下法ならではの問題もあるし。

勾配降下法の利用シーンはニューラルネットワークの学習などではあるが、
概念自体は関数の最小値の探索だ。
つまり、適当な関数を定義して、極小値目指して下っていく感じが見れればOK。

ここで問題になるのが「適当な関数」
ある程度の山や谷があるような関数が望ましい。
よって以下の関数を使うとする。

\(
\displaystyle f(x)=\sin(5x)+\frac{x^2}{2}
\)

これは三角関数と二次関数を合成したもの。
波形としては以下になる。

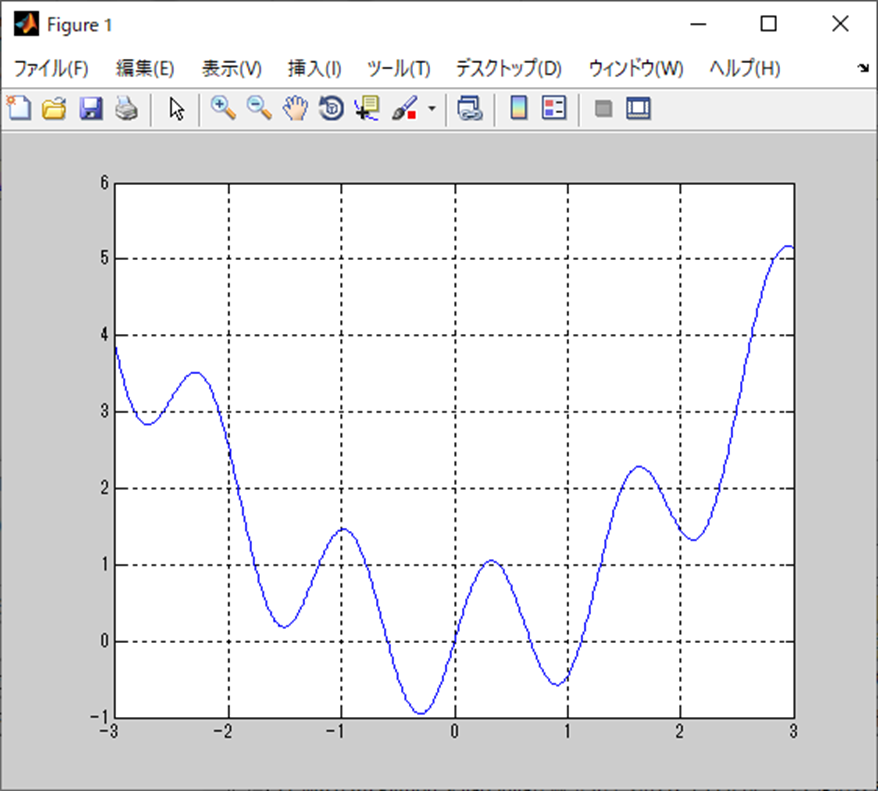
いい感じにナミナミしている。

傾きを知るためには導関数が必要。
先ほどの関数の導関数が以下になる。

\(
f(x)=5\sin(5x)+x
\)

三角関数の導関数を求める証明も存在するが、
今回の本筋ではないので、この証明は省略する。

次のページからプログラムの流れとか、それぞれの処理の詳細の話。