畳み込み積分の効能
そして、畳み込み積分の効能だが、
ガウシアンフィルタを実施する上ではノイズ除去になる。
試しにアニメーションgifを作成してみた。
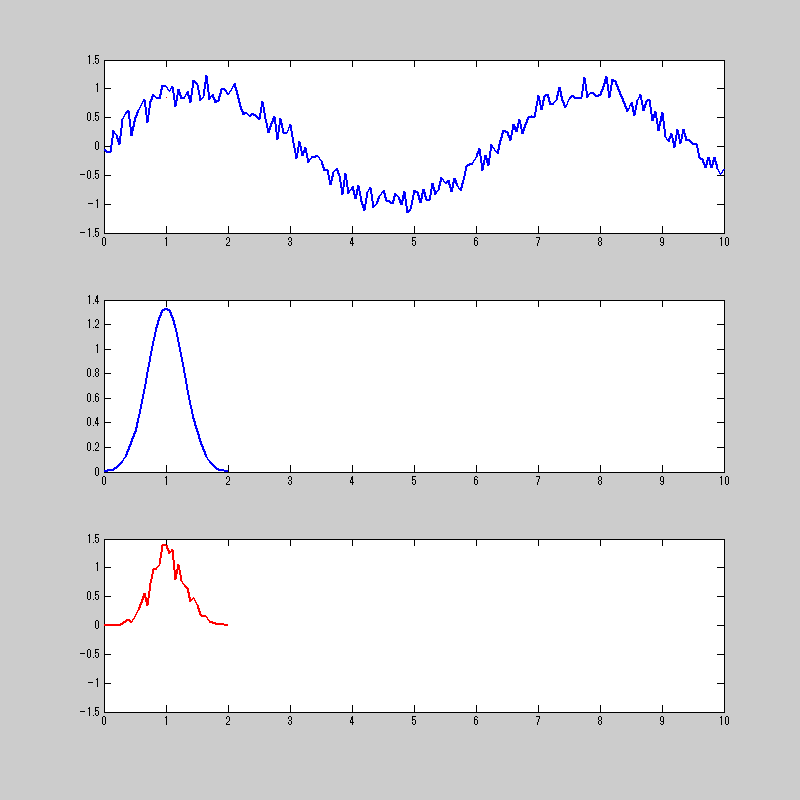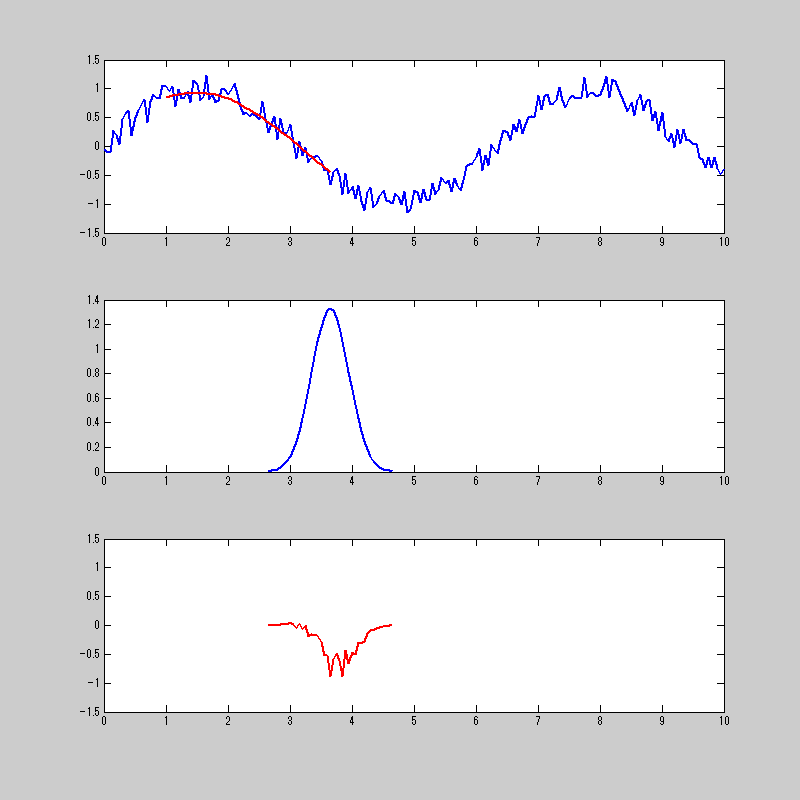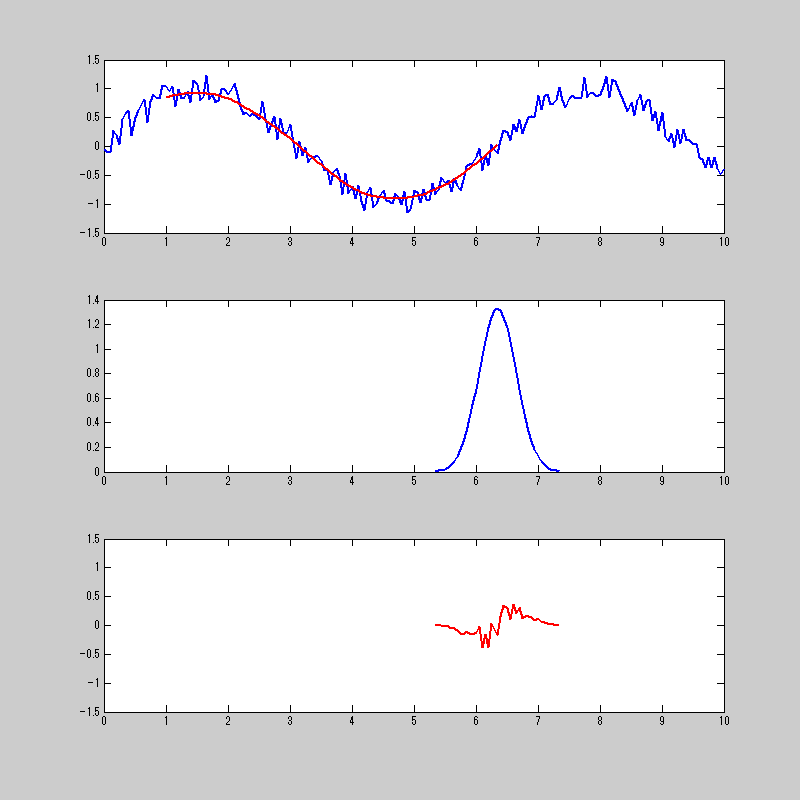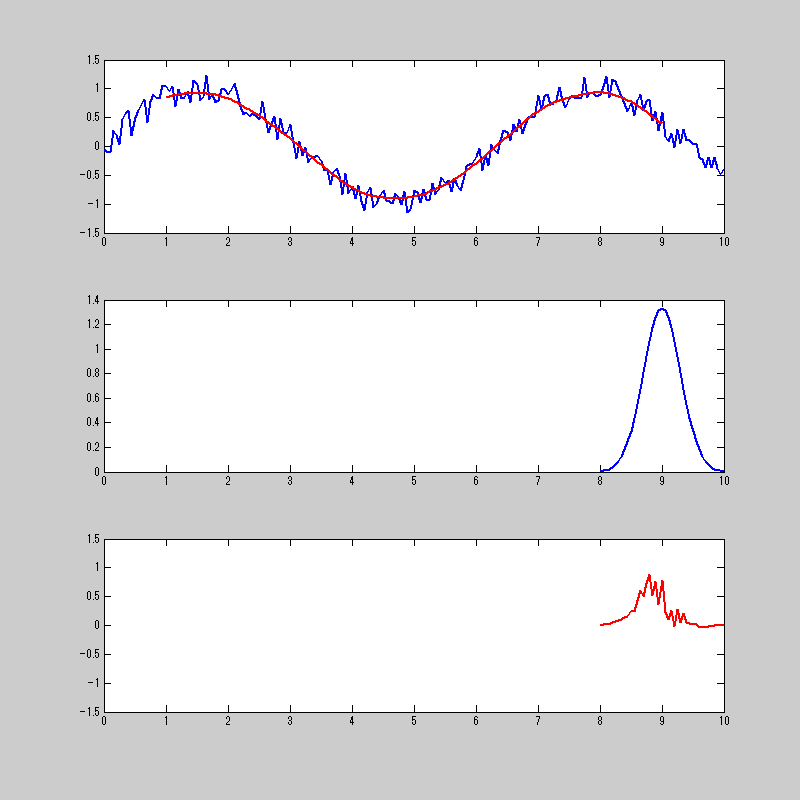
ミミズが暴れているだけのように見えるが・・・。
一番上が、元の信号と畳み込み積分をした結果。
二番目が、畳み込み積分をする関数
三番目が、元信号の関数と畳み込みをする関数を掛け合わせたもの。
三番目の信号を合計したものが1番上の赤の信号になる。
一番上のノイズが入った正弦波のノイズを除去してくれてる様子と思えば良い。
これは1次元空間の信号に対して畳み込み積分を実施しているのを表しているものだが、
これを2次元空間の画像に対して行うのが畳み込み演算。
つまり、1次元、2次元の違いはあるけど、概念的には同一のものということになる。
2次ガウス分布関数
2次ガウス分布関数について説明する。
先ほどの1次元の畳み込み積分を行ったときに使用したのが1次ガウス分布関数。
それの2次元版になる。
数式で書くとこんな感じ。
ちなみに\(\sigma\)は標準偏差。
\(
\displaystyle g(x,y,\sigma)=\frac{1}{\sqrt{2\pi\sigma}}\exp \bigg(-\frac{x^2+y^2}{2\sigma^2}\bigg)
\)
数式だけ書いても、ピンと来ないかもしれないが・・・。
2次ガウス分布関数を図で書くと？
とりえあず、2次ガウス分布の3×3と5×5の場合の具体的数値とそれをグラフにしたものを載せておく。
要は中心に重みが寄ってる山の形の関数ってことになる。
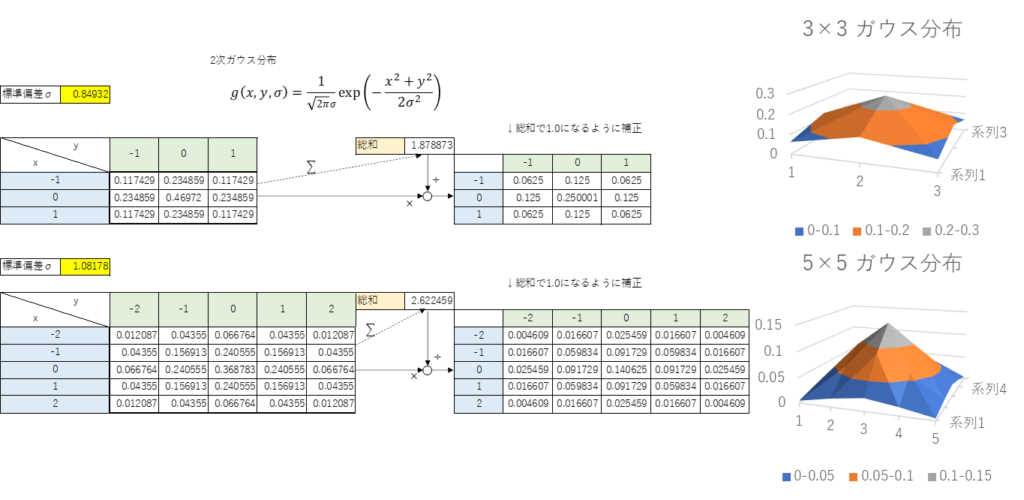
よく見ると妙な演算をしている。
総和を出したあとに、それで全体を割るっている。
これは、総和が1.0になるように補正を掛けてる。
総和が1.0になっていないと、畳み込み積分をした際に、元信号より増幅したり減衰したりする。
それを避けるための仕掛けになる。
良く使われるガウス分布カーネル
先ほど、2次ガウス分布関数を見せたが、実際は、これがそのまま使用されることは少ない。
一般的に利用される、代表的なガウス分布カーネルというものが存在する。
以下がそれになる。
\(
\displaystyle K_{3\times3}=\frac{1}{16}
\begin{bmatrix}
1 & 2 & 1 \\
2 & 4 & 2 \\
1 & 2 & 1 \\
\end{bmatrix}=
\begin{bmatrix}
0.0625 & 0.125 & 0.0625 \\
0.125 & 0.25 & 0.125 \\
0.0625 & 0.125 & 0.0625 \\
\end{bmatrix}
\)
\(
\displaystyle K_{5\times5}=\frac{1}{256}
\begin{bmatrix}
1 & 4 & 6 & 4 & 1 \\
4 & 16 & 24 & 16 & 4\\
6 & 24 & 36 & 24 & 6\\
4 & 16 & 24 & 16 & 4\\
1 & 4 & 6 & 4 & 1 \\
\end{bmatrix}\\=
\begin{bmatrix}
0.00390625 & 0.015625 & 0.0234375 & 0.015625 & 0.00390625 \\
0.015625 & 0.0625 & 0.09375 & 0.0625 & 0.015625\\
0.0234375 & 0.09375 & 0.140625& 0.09375 & 0.0234375\\
0.015625 & 0.0625 & 0.09375 & 0.0625 & 0.015625\\
0.00390625 & 0.015625 & 0.0234375 & 0.015625 & 0.00390625 \\
\end{bmatrix}
\)
2次ガウス分布関数を比較すると？
2次ガウス分布関数の画像と、先ほどの行列の値を見比べてみると分かるが、
かなり近い値になってる。
特に3×3の方はぴったり一緒と言って良いレベル。
というわけで、画像処理のガウシアンフィルターを実施する畳み込みカーネルは
この代表的な2つを使用することが多いってことになる。
多少の誤差があっても結果に対しては影響は少ないのだろう。
大量の小数を並べるより、スッキリするので、ここでも代表的な2次ガウス分布カーネルを採用する。
今後の方針
一通り、理屈に相当する話は終了。
あとは、実際に実験する話になる。
画像は以前から使用している「犬と自転車」
この画像に対してガウシアンフィルタを実施する。
しかし、今後の想定して、畳み込み演算をする関数を準備して、
画像と畳み込みカーネルを引数に渡せば畳み込み演算をしてくれるような仕様にするつもり。
というわけで具体的な処理の流れ
処理の流れは以下。
- 画像の読み込み
- RGB 3chに分解
- 畳み込み演算×3ch
- 画像とガウシアンカーネルを渡す。
- 画像保存
通常、グレースケールにして試すことが多いが、
特にやることが多いわけでもないので、
現時点ではRGBの3chに対して実施する予定。
同じことを3回やるだけなので。
まとめ
- ガウシアンフィルタについて説明。
- 畳み込み演算、畳み込み積分。
- 2次ガウス分布関数と近似の良く使われる2次ガウス分布カーネル。
- 実際に試す際は畳み込み演算の関数を作成予定。
MATLAB、Python、Scilab、Julia比較ページはこちら
コメント