【入門】微分方程式からCコードへ【数値計算】

MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
状態空間モデルをさらに掘り下げるために
状態空間モデルを使用せずに普通に微分解決すると？
運動方程式のブロック図(連続系)
運動方程式のブロック図(離散化)
漸化式
次のページへ

はじめに

の、
MATLAB,Python,Scilab,Julia比較その53【状態空間モデル⑪】
MATLAB,Python,Scilab,Julia比較その54【状態空間モデル⑫】
MATLAB,Python,Scilab,Julia比較その55【状態空間モデル⑬】

を書き直したもの。

本来のネタとしては「状態空間モデルの利用」ではあるのだが、
「状態空間モデルの利用しない場合はどうなるか？」の場合を想定した話となる。

対象モデルはシンプルさ重視でニュートンの運動方程式となる。

状態空間モデルをさらに掘り下げるために

状態空間モデルを掘り下げると、
ベクトル行列演算で微分解決する話になる。

その前に、
状態空間モデルを使用しない場合のシミュレーションのプロセスを大雑把に知っておいた方が良い。

状態空間モデルを使用せずに普通に微分解決すると？

状態空間モデルを使用せずに微分解決すると以下のような漸化式を導き出すことになる。

運動方程式
\(\boldsymbol{F}=m\boldsymbol{a} \)

加速度、速度、距離の関係
\(\boldsymbol{a}(t)=\boldsymbol{\dot{v}}(t)=\boldsymbol{\ddot{s}}(t) \)

速度の漸化式
\(\boldsymbol{\dot{v}}(t)=\displaystyle \frac{1}{m}\boldsymbol{F}(t)\)
\(\boldsymbol{v}(t)=\boldsymbol{\dot{v}}(t)\Delta T + \boldsymbol{v}(t-\Delta T) \)

距離の漸化式
\(\boldsymbol{\dot{s}}(t)=\boldsymbol{v}(t)\)
\(\boldsymbol{s}(t)=\boldsymbol{\dot{s}}(t)\Delta T + \boldsymbol{s}(t-\Delta T) \)

実際には、以下の手順をたどる。

ブロック図(連続系)
ブロック図(離散系)
漸化式
(フローチャート) → 企業によってあったりなかったり。今回は特にフローチャートは書かない
Cコード化
Cコードでシミュレーション

運動方程式のブロック図(連続系)

ブロック図(連続系)は以下となる。

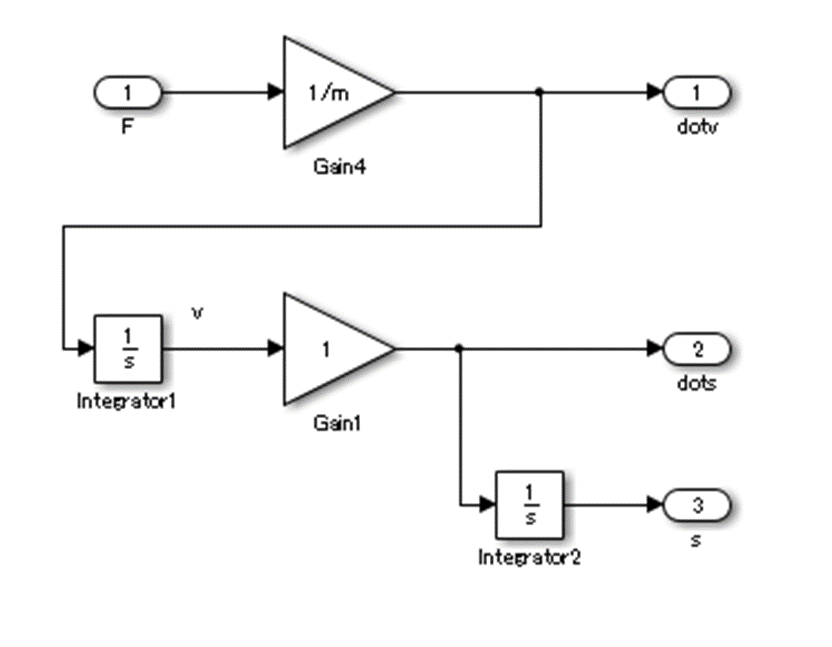
Simulinkであれば、この状態でシミュレーションは出来てしまう・・・。

運動方程式のブロック図(離散化)

上記のブロックを離散化すると以下になる。
積分器のところを加算器にさしかえるだけではある。
尚、微分解決の精度はテイラー1次相当になる。

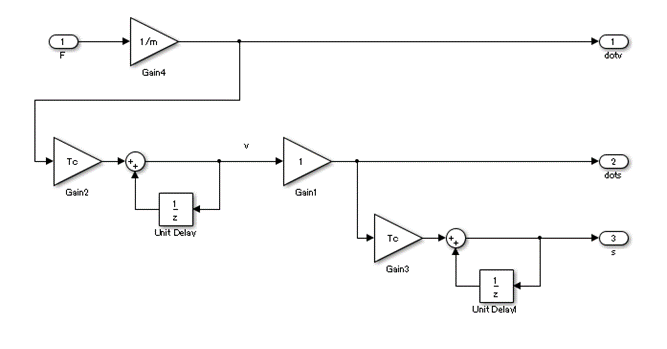
MATLAB/Simulinkであれば、ここからオートコード生成したりもする。

漸化式

上記のブロック図(離散化)を元に漸化式を求める。

速度の漸化式
\(\boldsymbol{\dot{v}}(t)=\displaystyle \frac{1}{m}\boldsymbol{F}(t)\)
\(\boldsymbol{v}(t)=\boldsymbol{\dot{v}}(t)\Delta T + \boldsymbol{v}(t-\Delta T) \)

距離の漸化式
\(\boldsymbol{\dot{s}}(t)=\boldsymbol{v}(t)\)
\(\boldsymbol{s}(t)=\boldsymbol{\dot{s}}(t)\Delta T + \boldsymbol{s}(t-\Delta T) \)

これでCコード化の準備が出来た状態となる。