MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その53【フーリエ級数(周期2L)⑥】
を書き直したもの。
フーリエ級数、フーリエ係数を周期2πを任意周期2Lに改造した。
これをScilabで実現する。
【再掲】フーリエ係数を求めるプログラムフロー
まずは、プログラムフローを再掲。
- csvファイル読み込み
- 各種変数初期化
- フーリエ係数算出
- n=10,50,200のパターンでフーリエ級数で波形を合成
- グラフにプロット
今回はフーリエ係数を求めるプログラムをScilabで実現。
【再掲】任意周期フーリエ級数、フーリエ係数
実現する数式はこれ
\(
\begin{eqnarray}
\displaystyle a_n&=&\frac{1}{L}\int_{-L}^{L}f(x)\cos(\frac{n\pi x}{L})dx\\
\displaystyle b_n&=&\frac{1}{L}\int_{-L}^{L}f(x)\sin(\frac{n\pi x}{L})dx\\
\displaystyle a_0&=&\frac{1}{L}\int_{-L}^{L}f(x)dx\
\end{eqnarray}
\)
Scilabコード
まず、使用する波形を取り込んだcsvファイル
Scilabコードは以下になる。
N=1000; // 係数算出項数(同定元波形のplotよりも少なく)
L=10; // 周期/2
wave=csvRead('wave.csv'); // 同定波形読み込み
points=length(wave); // 波形のplot数取得
fx=wave'; // 波形を行ベクトルへ
dx=2*L/points; // 1plotあたりのx軸幅
x=linspace(-L,L,points); // -π~+πの範囲で波形plot数分の等差数列
a = zeros(1,N); // a係数群格納用
b = zeros(1,N); // b係数群格納用
for n = 1:N
// 係数a_n算出
// a_n = (1/L)∫f(fx)cos(nxπ/L)dx
a(n) = fx*cos(n*x*%pi/L)'*dx/L;
// 係数b_n算出
// a_n = (1/L)∫f(fx)cos(nxπ/L)dx
b(n) = fx*sin(n*x*%pi/L)'*dx/L;
end
// 係数a_0算出
a0=sum(fx)*dx/L;
Ns = [10,50,200];
for i = 1:length(Ns)
NN = Ns(i); // 今回のa_n,b_n項数
// f(x)=a_0/2+Σ(a_n cos(nxπ/L)+ b_n sin(nxπ/L))
Fourier_series=ones(1,points)*a0/2;
for n = 1:NN
Fourier_series = Fourier_series+(a(n)*cos(n*x*%pi/L)+b(n)*sin(n*x*%pi/L));
end
// 元波形とフーリエ級数波形の表示
subplot(length(Ns),1,i);
plot(x, fx,'LineWidth',3);
plot(x, Fourier_series,'-r','LineWidth',2);
title(sprintf('n=%d',NN));
p=gca();p.tight_limits(:)="on";p.data_bounds(:,1)=[-L;L];
xgrid();
end処理結果
処理結果は以下。
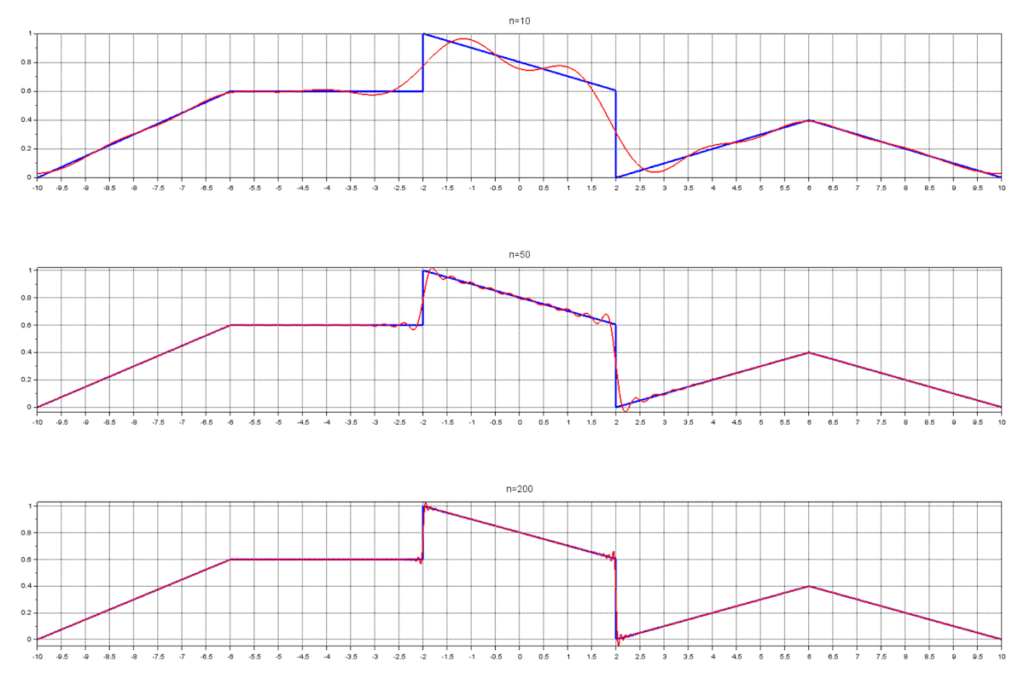
\(-\pi\sim\pi\)だけでなく、任意の周期を設定できることがわかる。
今回の場合は\(-10\sim10\)の範囲にしているが、当然変更することも可能。
まとめ
- フーリエ級数、フーリエ係数の任意周期版のプログラムをScilabで作成。
- -π~πだけでなく、-10~10のような任意の周期に適応可能。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす





コメント