波の合成
波の合成といっても名前からはいめーじできないかもしれない。
人によっては積分使いまくりとおもってしまうかもしれない。
結論としては
積分は使わない。
使うのは足し算。
もうちょっというと、三角関数の足し算。
波が必ず三角関数というわけではないが、
周期性を持つ代表的な関数が三角関数であることと、
フーリエ級数に繋げる場合は、三角関数の合成の方が話としては近い。
というわけで、
波の合成≒三角関数の足し算
と思って良いだろう。
一点例を出すと以下になる。
\(
sin(x)+sin(2x)+sin(3x)
\)
波の合成結果
際ほどは波の合成の例を数式で示したのみ。
これが具体的にどのような波形になるのか確認しておこう。
以下になる。
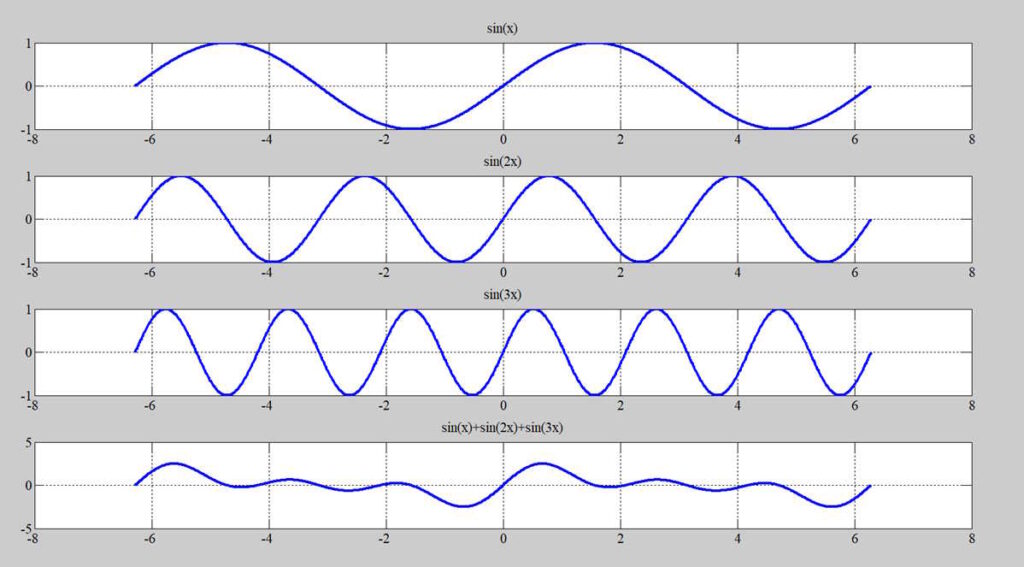
上から、sin(x)、sin(2x)、sin(3x)。
一番下がそれらを合成したもの。
それぞれの単体の波形は当然のことながらシンプルだが、
合成すると複雑になっていくことになる。
これがフーリエ級数にとって重要な事象となる。
まとめ
- フーリエ解析学は「フーリエ級数、係数」と「フーリエ変換、逆フーリエ変換」に分けられる。
- 「フーリエ級数、係数」も実数フーリエと複素フーリエに分けらえる。
- 無限級数について説明。
- 波の合成について説明。
- 単なる関数の足し算になる。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
Amazon.co.jp
amzn.to
手を動かしてまなぶ フーリエ解析・ラプラス変換
Amazon.co.jp
amzn.to
物理数学 量子力学のためのフーリエ解析・特殊関数
物理数学 量子力学のためのフーリエ解析・特殊関数 | 柴田 尚和, 是常 隆 | 数学 | Kindleストア | Amazon
Amazonで柴田 尚和, 是常 隆の物理数学 量子力学のためのフーリエ解析・特殊関数。アマゾンならポイント還元本が多数。一度購入いただいた電子書籍は、KindleおよびFire端末、スマートフォンやタブレットなど、様々な端末でもお楽しみい...
amzn.to
単位が取れるフーリエ解析ノート
https://amzn.to/3V83fIl
amzn.to
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす
https://amzn.to/3ysbfvf
amzn.to
コメント