MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その37【フーリエ係数①】
MATLAB,Python,Scilab,Julia比較 第5章 その38【フーリエ係数②】
を書き直したもの。
フーリエ係数に至る道。
今回からフーリエ係数の話に突入。
三角関数の直交性を利用した成分抽出の話になる。
【再掲】フーリエ係数に至る道
まずは、フーリエ係数に至る道を再掲。
- 偶関数
- 奇関数
- 関数の内積
- 三角関数の加法定理
- 三角関数の積和公式
- 重要な極限値
- 三角関数の直交性
- フーリエ係数
今回からフーリエ係数の話に突入する。
前回までに求めた三角関数の直交性を示す公式
フーリエ係数を求めるうえで重要なのが、
前回までに求めた三角関数の直交性を示す公式達になる。
この式になる。
\(
\begin{eqnarray}
&&\displaystyle\int_{-\pi}^{\pi}\sin(mx)\cos(nx)dx=0\\
&&\displaystyle\int_{-\pi}^{\pi}\sin(mx)\sin(nx)dx=
\cases{
\pi\dots \text{if } n=m\\
0\dots\text{if } n\neq m
}\\
&&\displaystyle\int_{-\pi}^{\pi}\cos(mx)\cos(nx)dx=
\cases{
\pi\dots \text{if } n=m\\
0\dots\text{if } n\neq m
}
\end{eqnarray}
\)
この公式により、\(\sin,\cos\)が直交していることの証明と
\(\sin\cdot\sin\)、\(\cos\cdot\cos\)、の解が\(0\)か\(\pi\)になることが証明された状態となる。
ベクトルの成分を抽出する理屈
フーリエ係数を求める上で、ベクトルからの成分抽出というのが重要な考え方となる。
例えば、\((a,b)\)というベクトルがあり、
これの成分である\(a,b\)をそれぞれ抽出するにはどうすれば良いか。
答えとしては、基本ベクトルとの内積を求めればOKという話となる。
基本ベクトルは、\((1,0)\)、\((0,1)\)みたいなもの。
試しに図も交えながら、\(a,b\)が抽出されるイメージをとらえてみよう。
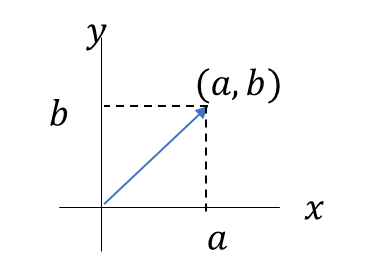
\(
\begin{eqnarray}
\begin{bmatrix}
a&b
\end{bmatrix}
\begin{bmatrix}
1\\0
\end{bmatrix}=a\\
\begin{bmatrix}
a&b
\end{bmatrix}
\begin{bmatrix}
0\\1
\end{bmatrix}=b
\end{eqnarray}
\)
というわけで\(a,b\)が抽出できる。
この感覚を別の軸且つ多変量な空間に対して行うのがフーリエ係数を求めるためのベクトルの内積となる。
次のページへ
次のページでは、実際に三角関数の直交性を利用した三角関数成分の抽出をやってみる。





コメント