決定境界直線
分類問題の説明の時にも出たが、
分類は、平面または空間上での分類を行う線を求めることが目的となる。
以前の分類問題の説明の時の犬と猫を仕訳けてる線になる。
こういう線のことを決定境界線という。
今回の場合は、線形分類なので、
決定境界直線ということになる。
ANDゲートの場合の想定される決定境界直線
ANDゲートの場合のどのような感じになるか確認しておこう。
ANDゲートの入力を横軸、出力を縦軸にしたグラフで表現すると以下のようになる。
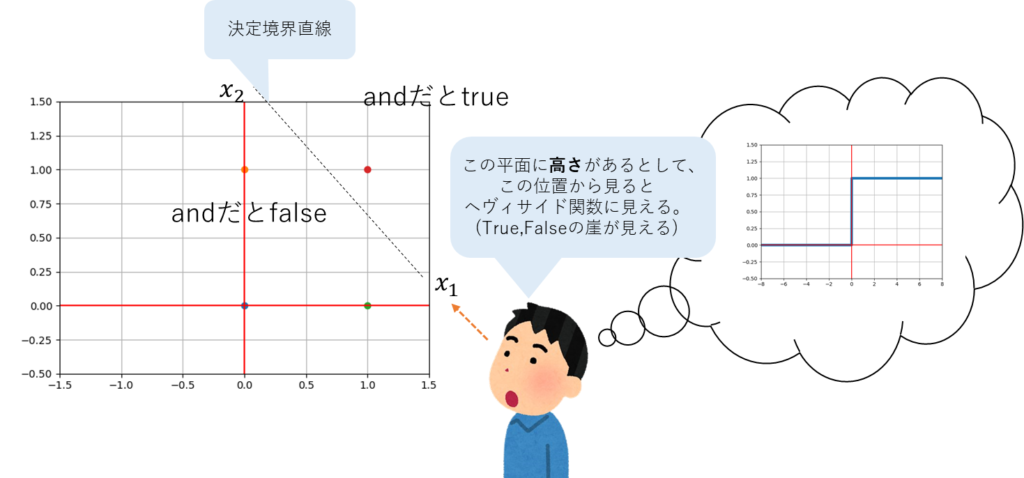
決定境界直線より上が1、つまりtrue。
決定境界直線より下が0、つまりfalse。
ってことになる。
このtrueとfalseの出力を表現するためにヘヴィサイド関数が使われている。
こんな感じで、明確にtrue、falseを表現できるのがヘヴィサイド関数の利点になる。
決定境界直線の必要性
実は・・・。
分類をする上では、決定境界直線そのものはしらなくても分類は実現可能。
決定境界直線を決定づけるのは学習したモデル。
その学習済みの完成したモデルに対して推論を行わせるには
単純に入力を入れればOK。
利用する側が決定境界直線を意識することはない。
というわけっで、利用するだけだったら無視してもOK。
しかし、学習結果としてどこに決定境界直線が引かれているかは見えてないと
その境界線が適切かがわからない。
つまり、学習後のモデルの性能を見る上では重要ってことになる。
結局、今回に於いては必要と位置づけになる。
どこに境界線を引いたかは作る側からしたら重要になるので。
決定境界直線の特定方法
再掲になるが、今回、分類を行うモデルは以下になる。
\(
y=H\Bigg(
\begin{bmatrix}
w_1&w_2&b
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
1
\end{bmatrix}
\Bigg)
\)
そして、境界線はヘヴィサイド関数がどのような出力をしたときのものになるだろうか?
境界線なので、ヘヴィサイド関数が0から1、または1から0に変化した時になる。
ただし、これだと数式上で境界線の特定が困難。
ヘヴィサイド関数としてはあり得ない出力だが、
0と1の間の0.5の出力した時が境界線上と仮定しよう。
グラフで表現すると以下の感じになる。
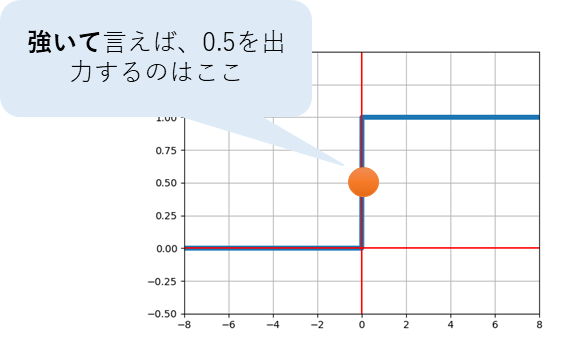
ヘヴィサイド関数が0.5を出力するのは入力が0の時。
つまり以下の式が成り立つ
\(0.5=H(0)\)
少なくとも関数の入力と出力の関係で見れば正しい。
ヘヴィサイド関数の入力が0の時に決定境界直線上にあると言えるので、以下の式を解いていく。
\(
\begin{eqnarray}
0&=&
\begin{bmatrix}
w_1&w_2&b
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
1
\end{bmatrix}\\
0&=&w_1x_1+w_2x_2+b\\
w_1x_1&=&-w_2x_2-b\\
x_2&=&-\frac{w_1x_1+b}{w_2}
\end{eqnarray}
\)
よって、
\(w_1,w_2,b\)が求まった後であれば、
\(x_1\)から\(x_2\)が求まる。
ここでの\(x_2\)は\(y=0.5\)を満たす決定境界直線を示すものとなる。
次のページへ
次のページで実際にプログラミングをする際のフローを記載



コメント