HelloWorld
よくプログラムをする際に
標準出力方法を最初に学ぶことが多い。
「HelloWorld」とか出力するあれ。
分類問題の於けるHelloWorld相当というものがある。
と言っても、「HelloWorld」という文字列を表示するわけでは無く、
最も基本的且つ最もシンプルな話。という意味合い。
分類問題のHelloWorld
分類問題の於けるHelloWorldは、
ANDゲートになる。
ANDゲートって、2入力あり、
両方が1なら1、どちらかが0だったら0になる。
という入力出力の関係を取った論理ゲート。
真理値表で表現するとこうなる。
ANDゲートの真理値表
| \(x_1\) | \(x_2\) | \(y\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2入力1出力の形式ニューロン
この際のANDゲートを、形式ニューロンで表現したい。
この場合の形式ニューロンは
2入力1出力の構成になる。
概念図で示すと以下になる。
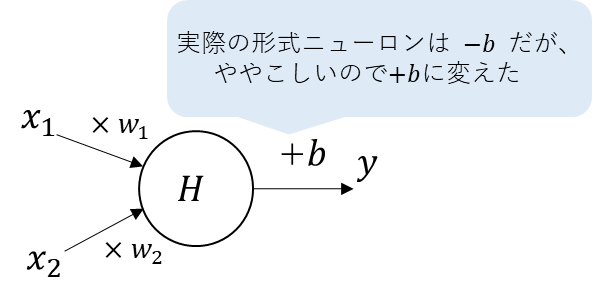
形式ニューロンのバイアスは、本来であれば\(-b\)で表現されるが、
話をシンプルにするために\(+b\)に表現しなおしている。
(毎回マイナスを意識するのも面倒なので・・・)
そして、これを数式で表現すると以下になる。
\(
y=H\Bigg(
\begin{bmatrix}
w_1&w_2&b
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
1
\end{bmatrix}
\Bigg)
\)
先の概念図、数式からすると分かると思う。
この構成をもって、適切な\(w_1,w_2,b\)を探すことが、分類問題を解く。
ということになる。
代表的な誤差関数
ここでは、誤差関数について説明する。
誤差関数は、回帰分析の時にも出てきた言葉。
回帰分析の時は、目的の結果と実際の推論の差で0になればOKってやつだった。
今回の誤差関数もイメージ的には同じ。
ただし、
回帰の場合は、0になる点を特定するという発想だったが、
分類問題置いては必ず0の点が見つかるとは限らない。
よって、可能な限り誤差関数の結果が小さいところを最適解する。
って考え方になる。
とりあえず、代表的な誤差関数を紹介しておこう。
平均二乗誤差(MSE:Mean Squared Error)
\(
\begin{eqnarray}
MSE&=&\displaystyle\frac{1}{n}\sum_{i=1}^n(\hat{y_i}-y_i)^2\\
&=&\frac{1}{データ数}\sum_{i=0}^n(予測値_{i番目}-正解値_{i番目})^2
\end{eqnarray}
\)
二乗和誤差関数(SSE:Sum of Squared Error)
\(
\begin{eqnarray}
SSE&=&\displaystyle\sum_{i=1}^n(\hat{y_i}-y_i)^2\\
&=&\sum_{i=0}^n(予測値_{i番目}-正解値_{i番目})^2
\end{eqnarray}
\)
二乗平均平方根誤差(RMSE:Root Mean Squared Error)
\(
\begin{eqnarray}
RMSE&=&\displaystyle\sqrt{\frac{1}{n}\sum_{i=1}^n(\hat{y_i}-y_i)^2}\\
&=&\sqrt{\frac{1}{データ数}\sum_{i=0}^n(予測値_{i番目}-正解値_{i番目})^2}
\end{eqnarray}
\)
今回使用するのはMSE。
これは、計算式的に分散と一緒。
統計学として意味のある誤差の値になる。
という性質がある。
SSEは、回帰分析で使用したものになる。
\(SSE=\displaystyle\frac{1}{2}\sum_{i=1}^n(\hat{y_i}-y_i)^2\)
のように変形したものが
使用される場合もある。
微分した際に1/2が消えてくれて数式がきれいになり、
シンプルなため数学的テクニックを盛り込みやすい。
似たような感じだけど、それぞれ性質とか目的が違う。
これら以外にも大量にあるが、基本は、予測値と正解値の差を評価したいという意味では一緒。
次のページへ
次のページから、決定境界線の話



コメント