MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第4章 その3【形式ニューロン①】
MATLAB,Python,Scilab,Julia比較 第4章 その4【形式ニューロン②】
MATLAB,Python,Scilab,Julia比較 第4章 その5【形式ニューロン③】
MATLAB,Python,Scilab,Julia比較 第4章 その6【形式ニューロン④】
MATLAB,Python,Scilab,Julia比較 第4章 その7【形式ニューロン⑤】
MATLAB,Python,Scilab,Julia比較 第4章 その8【形式ニューロン⑥】
MATLAB,Python,Scilab,Julia比較 第4章 その9【形式ニューロン⑦】
を書き直したもの。
今回から形式ニューロンについての解説に突入。
おおよそ以下の無いようになる。
- 形式ニューロンについての解説。
- 形式ニューロンの概念図とか数式とか。
- 形式ニューロンについての解説。
- 分類問題のHelloWorldに相当する話。
- 今回は誤差関数について説明。
- 今回は決定境界直線について説明。
- 今回は決定境界直線の特定方法について説明。
- 今回は総当たり法による分類について説明。
形式ニューロンに至る道
まずは形式ニューロンを解説する。
ただし、単に形式ニューロンだけの説明で終わる感じじゃない。
複数の知識の組み合わせで成立すると思った方が良い。
というわけで、ロードマップを提示しておく。
- ヘヴィサイド関数
- 形式ニューロン
- 分類問題のHelloWorld
- 誤差関数
- 決定境界直線
- 決定境界直線の特定方法
- 総当たり法による分類
ヘヴィサイド関数
まずはヘヴィサイド関数。
これが形式ニューロンの性格を顕著に表すものと言って良いだろう。
どのような関数を知るために、まずはWikipediaから引用。
ヘヴィサイドの階段関数(、英: Heaviside step function)は、正負の引数に対しそれぞれ 1, 0 を返す階段関数である。名称はオリヴァー・ヘヴィサイドにちなむ。ヘヴィサイド関数と呼ばれることもある。通常、H(x) や Y(x) などで表されることが多い。
Wikipediaより(https://ja.wikipedia.org/wiki/%E3%83%98%E3%83%B4%E3%82%A3%E3%82%B5%E3%82%A4%E3%83%89%E3%81%AE%E9%9A%8E%E6%AE%B5%E9%96%A2%E6%95%B0)
これだけ見てもわからないかもしれない。
よって、グラフも示す。
連続系を非連続系に変換する関数の最もシンプルなもの。
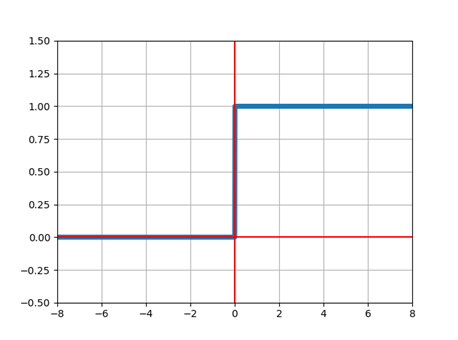
正の入力だと1、負の入力だと0ってことになる。
この関数の性格を利用すると、
もやっとしたものをYes/Noに変換できるとと思っておけば良いだろう。
形式ニューロンの概念図
形式ニューロンの概念図を示す。
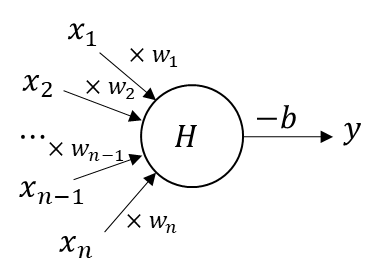
\(x\)が入力ベクトル、
\(y\)が出力、
\(w\)が重み、
\(b\)がバイアス
\(H\)がヘヴィサイド関数
になる。
ニューラルネットワークの説明でよく見る画像に似ていると思う。
違いとしては、
バイアスが負になってる点と
活性化関数がヘヴィサイド関数ってところ。
形式ニューロンの数式表現
形式ニューロンの数式表現も載せておこう。
\(
y=H\Bigg(
\begin{bmatrix}
w_1&w_2&\dots&w_{n-1}&w_n&-b
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
\vdots\\
x_{n-1}\\
x_n
\end{bmatrix}
\Bigg)
\)
その結果をヘヴィサイド関数に渡して、0 or 1を出力するって仕組みになる。
よく聞くニューロンの振る舞いはここからきている。
ただし、この構成はいろいろ問題があるから、現在に於いてはほぼ使われてはいない。
パーセプトロン、ニューラルネットワークの基本構成の元にはなってるという位置づけになる。
次のページへ
次のページから最も簡単な分類問題の話とか





コメント