MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その7【偶関数と奇関数①】
MATLAB,Python,Scilab,Julia比較 第5章 その8【偶関数と奇関数②】
を書き直したもの。
フーリエ係数に至る道。
今回は偶関数の説明。
フーリエ係数とフーリエ係数
前回で、フーリエ級数の話が終わり、
今回からフーリエ係数の話になる。
フーリエ級数とフーリエ係数って名前は似てるが、
基本別物になる。
前回も言ったが、フーリエ係数は、フーリエ級数内にある係数を求めるための処理。
関係性は深いが、処理自体は別物になる。
これもいろいろ前提知識が必要になるのが問題。
フーリエ係数へ至る道
というわけで、フーリエ係数に至る道を示しておこう。
- 偶関数
- 奇関数
- 関数の内積
- 三角関数の加法定理
- 三角関数の積和公式
- 重要な極限値
- 三角関数の直交性
- フーリエ係数
フーリエ級数の時と比べて異様に多い。
大半の知識は「三角関数の直交性」に必要な知識になる。
つまり、「フーリエ係数」自体は「三角関数の直交性」を利用したアプローチと言うことになる。
途中で数学パズルっぽいのもあるかも?
偶関数と奇関数に関しては、
かなり特徴的な関数の性質。
この特徴を利用した数学パズルみたいなのもやる予定。
どのようなパズルかと言うと、普通だったら解けなさそうなものを、裏技的に解いちゃう感じ。
余談に近い部分だから気軽に見てもらえればOK。
偶関数の定義
まずは偶関数から。
定義についてはWikipediaから引用する。
関数\(f(x)\)が偶関数であるとは、
Wikipediaより(https://ja.wikipedia.org/wiki/%E5%81%B6%E9%96%A2%E6%95%B0%E3%81%A8%E5%A5%87%E9%96%A2%E6%95%B0)
\(f(-x)=f(x)\)
が任意の\(x\)について成立することである。
何言ってるのかわけわからん感じだが、
要は、
\(y\)軸\(x\)は\(0\)に対して線対称になるのが偶関数。
ということになる。
偶関数の例
偶関数の例を示した方が早そうだろう。
代表的なものは以下2つ。
\(y=x^n\dots(ただしnは偶数であること)\)
\(y=\cos(x)\)
実際のグラフはこれになる。
\(y=x^4\)
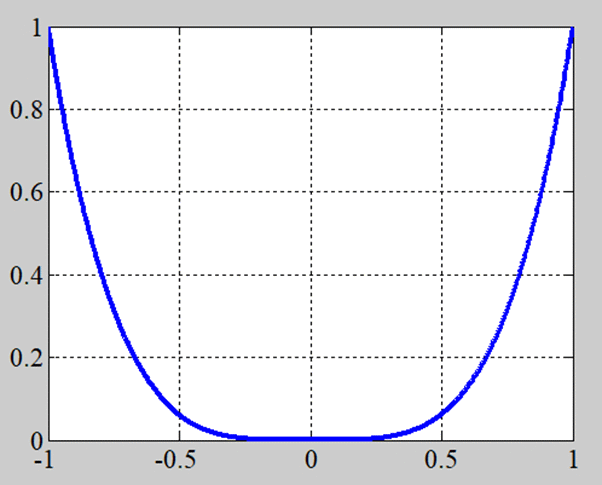
\(y=\cos(x)\)
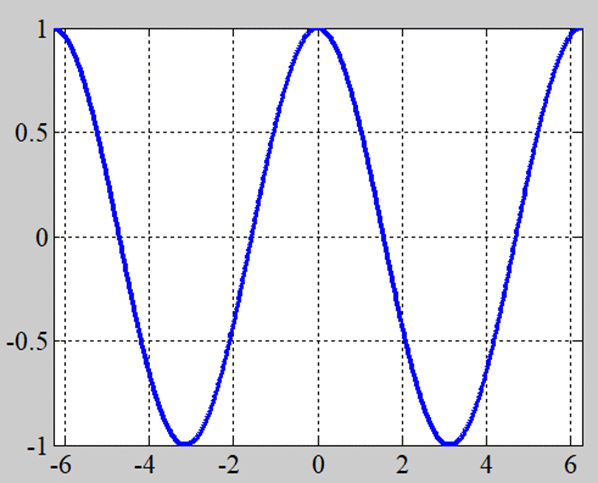
\(y\)軸に対して線対称ということがわかるだろう。
偶関数の特性
ここで偶関数に重要な特性がある。
\(x=0\)を中心として\(-L\sim L\)の範囲で定積分した場合と、
\(0\sim L\)の歯に出定積分したものを2倍にした値は同一。
という特性
これは\(y\)軸に対して線対称になるところから当たり前の特性ではあるが。
当然、この特性を利用することになるから、
まずは偶関数というものがあり、線対称であり、定積分した際は片方の定積分の2倍の関係になる。
と覚えておけばOK。
まとめ
- フーリエ係数の話に突入。
- フーリエ係数へ至る道を説明。
- 偶関数について説明。
- 単純にy軸に対して線対称な関数。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす





コメント