【入門】最小二乗法の初歩【数値計算】

誤差関数の最小値を求めるには？(2回目)

偏微分を用いて求めたい\(a\)と\(b\)を特定する。
\(a\)に於いての偏微分が0、\(b\)に於いての偏微分が0の部分が最小二乗法で欲しい\(a,b\)の条件となる。
式にすると以下になる。

\(
\displaystyle \frac{\partial L(a,b)}{\partial a}=0,\frac{\partial L(a,b)}{\partial b}=0
\)

偏微分で記載しているが、ここでは普通の微分と捉えてOKだ。

この偏微分は一体何を示しているのだろうか？

\(a\)と\(b\)を総当たりで値を振ったときを思い出してほしい。
両方とも、2次関数的な軌跡を描いていたと思う。

というわけで、その双方が最小値になった時がもっとも誤差が小さいときと言える。
図で説明する以下になる。

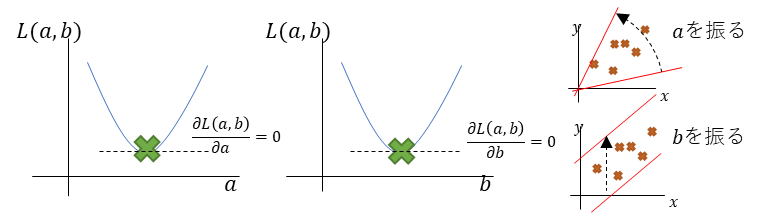
微分の性質として、0になる点は極大値か、極小値。
最小二乗法に於いては必ず極小値になる。
よって、偏微分して0が誤差が最も少ない点。
という理屈が作れる。

偏微分で誤差関数の最小値が求められるというのは理解できたが、
そもそも具体的な値として求められるものなのか？
という感じでイメージが沸かないこともあるだろう。

結論としては、
誤差関数自体はすでに求まっているので、
それに対して偏導関数を導出するだけになる。

偏導関数の求め方を簡単に説明しておこう。

偏導関数については対して難しくはない。
基本的には導関数の求め方と一緒で、偏微分する軸以外は定数と見なす。
まずは導関数の求め方を復習も兼ねて示しておこう。

これは高校数学の1年生くらいで習うものだと思うけど、
以下の公式がある。

\(
\displaystyle x^n\frac{d}{dx}=nx^{n-1}
\)

先のルールは偏導関数でも一緒になる。

\(
\displaystyle \frac{\partial x^n}{\partial x}=nx^{n-1}
\)

これだけ見ると全く一緒に見えるだろう。
ここに\(x\)とは別の変数として\(y\)を追加すると、以下になる。

\(
\displaystyle \frac{\partial (x^n＋x^2y+y^2)}{\partial x}=nx^{n-1}+2yx
\)

\(y^2\)が消えて、\(x^2y\)は\(y\)に関してはそのまま残ってる。
これは\(y\)は変数だけど、偏導関数を求める際は定数と見なしてるため。
つまり、\(y^2\)は\(x\)と無関係だから消えるし、\(x^2y\)は\(x\)に関わる部分だけ導関数が求まる。

今回のは比較的簡単な例ではあるが、
\(x,y\)両方の動きを合わせて微分するより偏微分した方が楽だというのはわかったと思う。

今回偏微分しようとしてる誤差関数ってΣが式に入ってる。
一見すると、これの扱いがめんどそうな気がするかもしれない。

結論から言うとΣは気にしなくてよい。
例えば、以下の式を考えよう。

\(
\displaystyle\frac{\partial\sum x_i^2}{\partial x}
\)

これの微分のイメージはわかないかもしれない。
こうしたらどうだろうか？

\(
\displaystyle\frac{\partial(x_1^2+x_2^2+x_3^2+\dots+x_n^2)}{\partial x}
\)

それぞれの導関数が\(2x_n\)になるから、以下の考え方になる。

\(
\begin{eqnarray}
\displaystyle\frac{\partial\sum x_i^2}{\partial x}&=&2x_1+2x_2+2x_3+\dots+2x_n \\
&=&\sum2x_i=2\sum x_i
\end{eqnarray}
\)

この考え方で解けばΣが入った式も怖くないはず。