MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第2章 その2【最小二乗法①】
MATLAB,Python,Scilab,Julia比較 第2章 その3【最小二乗法②】
MATLAB,Python,Scilab,Julia比較 第2章 その4【最小二乗法③】
MATLAB,Python,Scilab,Julia比較 第2章 その5【最小二乗法④】
MATLAB,Python,Scilab,Julia比較 第2章 その6【最小二乗法⑤】
MATLAB,Python,Scilab,Julia比較 第2章 その7【最小二乗法⑥】
を書き直したもの。
1次関数の最小二乗法についての説明をする。
1次関数の最小二乗法
まずは1次関数の最小二乗法から説明していこう。
これはもっともシンプルな回帰分析と言える。
最小二乗法は、複数のプロットを元に最もそれらしい線を引く。
ってのを実現しているもの。
その「最もそれらしい線」っていうのをどう特定しているのか?
ってのがポイントとなる。
最もそれらしい線の特定方法
「最もそれらしい線」の特定方法は、
各サンプリングとの誤差が最小となる線となる。
以下のイメージになる。
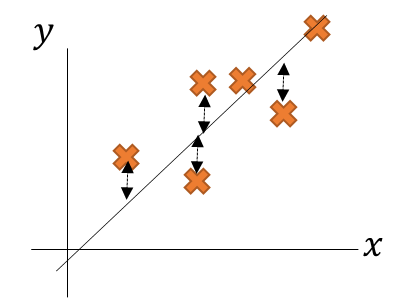
そして、「誤差が最小」という部分だが、
単純に引き算で求めると、サンプリングと線の位置関係が上か下かで符号が逆転してしまう。
それを抑制するために「誤差の二乗の和が最小になる線」を特定することになる。
二乗にすれば、符号の問題は無くなる。
この手法から最小二乗法という名前になっている。
誤差関数
そして、「誤差の二乗の和が最小になる線」を求める際に最小を目指すための関数を誤差関数と呼ぶのだが、
1次関数の最小二乗法にとっての誤差関数を特定する必要がある。
まず、以下が誤差が最小の関数であると仮定する。
(普通の一次関数)
\(ax+b=y\)
サンプリングした\((x,y)\)を元に\((a,b)\)を求めたいので、
最小化したい誤差関数\(L\)を求める。
\(
\begin{eqnarray}
L(a,b)&=&\displaystyle\sum_{i=0}^n\{y_i -(ax_i +b)\}^2 \\
&=&\displaystyle a^2\sum x_i^2+nb^2+\sum y_i^2-2a\sum x_i y_i -2b\sum y_i +2ab\sum x_i
\end{eqnarray}
\)
一見するとややこしいかもしれないが、
これが最終的にはシンプルになる・・・はず。
nb^2について
さっきの誤差関数の中に\(nb^2\)ってのがいたが、これについて説明しておく。
これは、以下の変形をした結果になる。
\(
b^2\sum 1=nb^2
\)
\(\sum 1\)って丁寧に書くと以下になる。
\(
\displaystyle\sum_{i=1}^5=1+1+1+1+1=5
\)
n個の1の和だから、nになると思えばOK。
誤差関数の最小値を求めるには?
誤差関数を最小化される\((a,b)\)を求める必要がある。
総当たりで求めるというのも一つの考え方になる。
求めたい一次関数於いて、\(a\)が傾き、\(b\)が切片なので、
適当にプロットした点に対して、それぞれを動かした場合の誤差関数\(L\)の値を見てみよう。
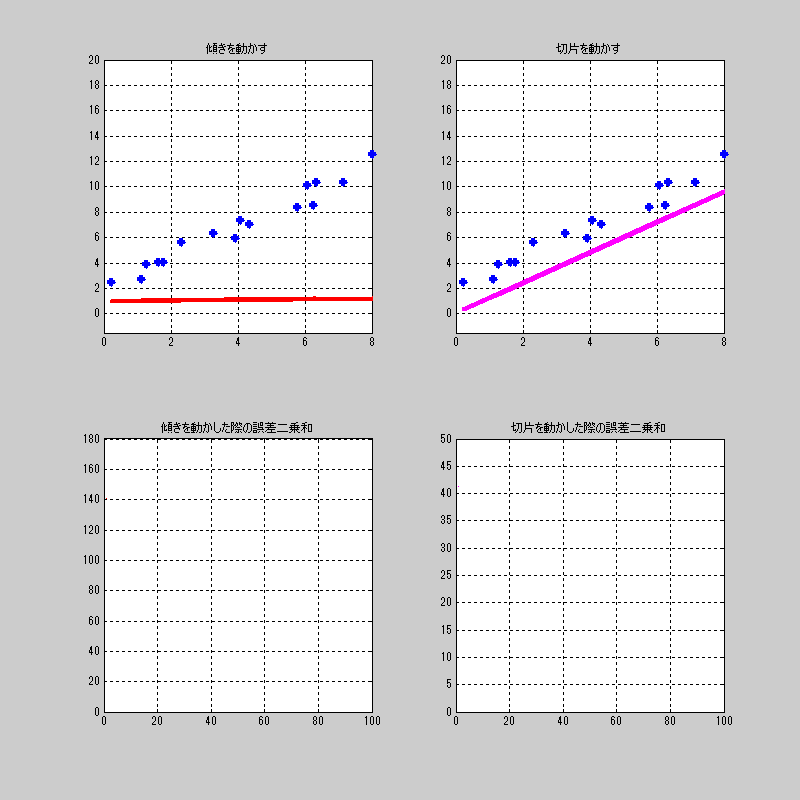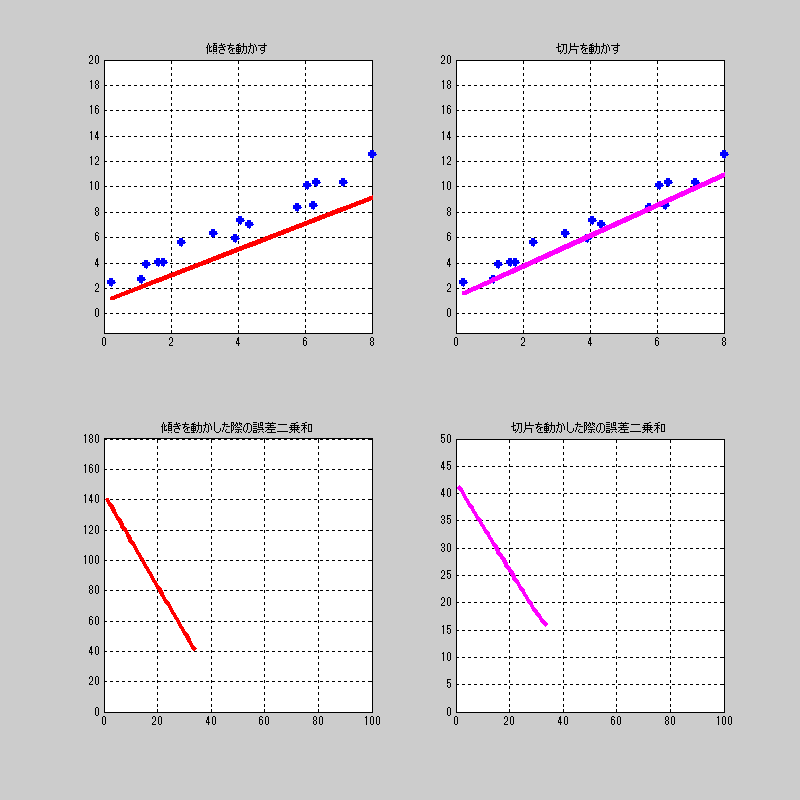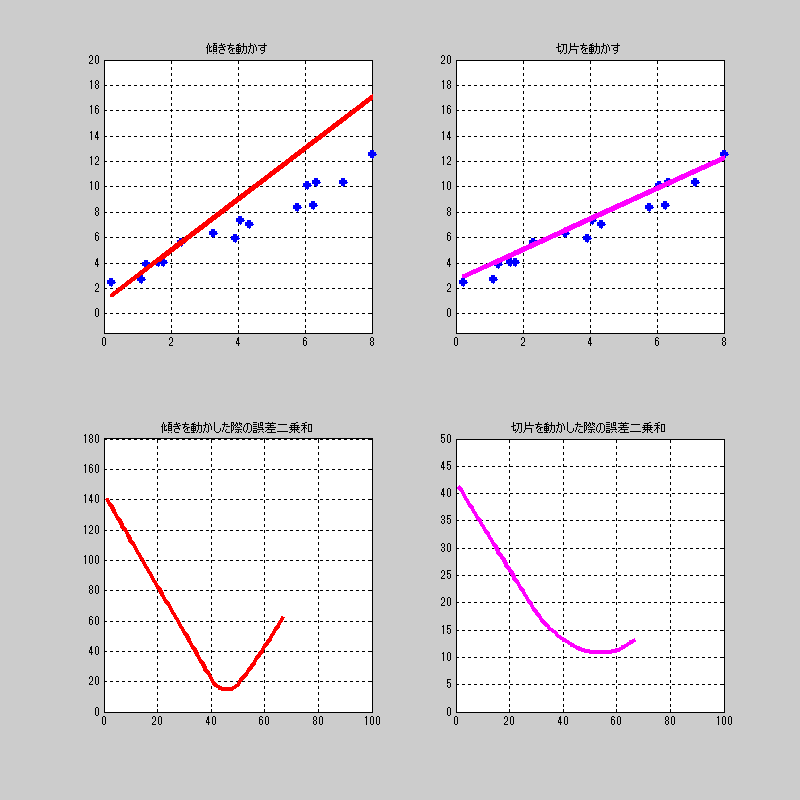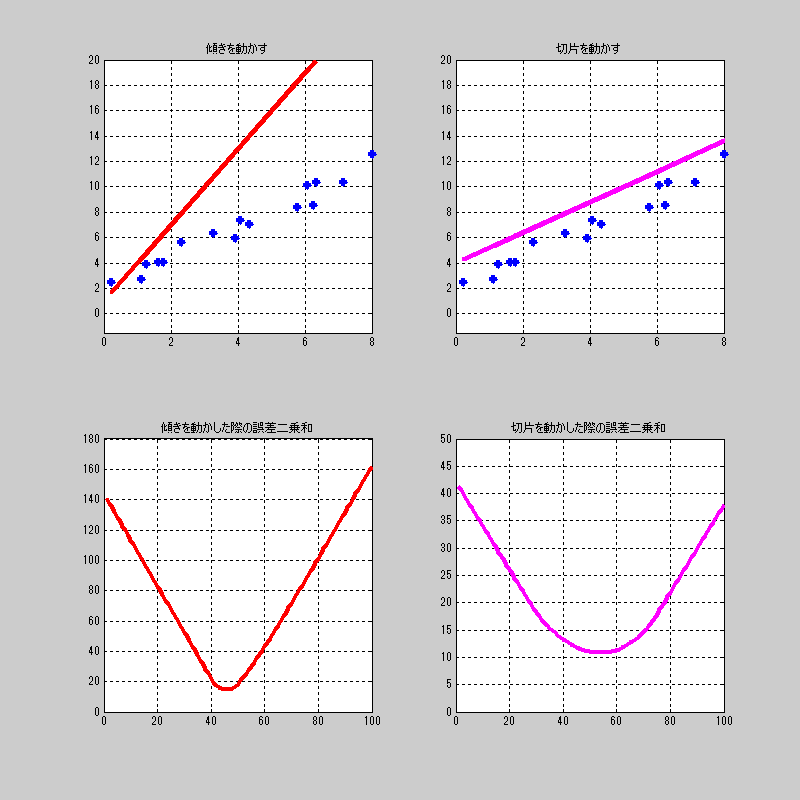
誤差関数を総当たりしてる雰囲気
先ほどの動画は、傾きだけを動かした場合、切片だけを動かした場合で、
実際の総当たりは、もっと大量の検査をすることになる。
ここでは切片をちょっと動かして、それに対して、傾きを総当たり。
を繰り返す画像を見せよう。
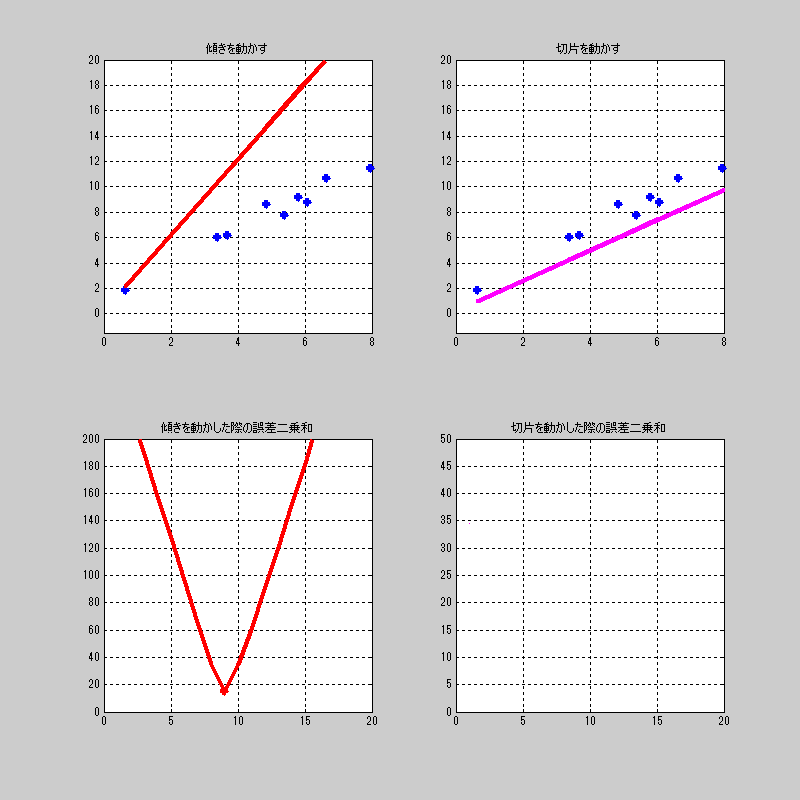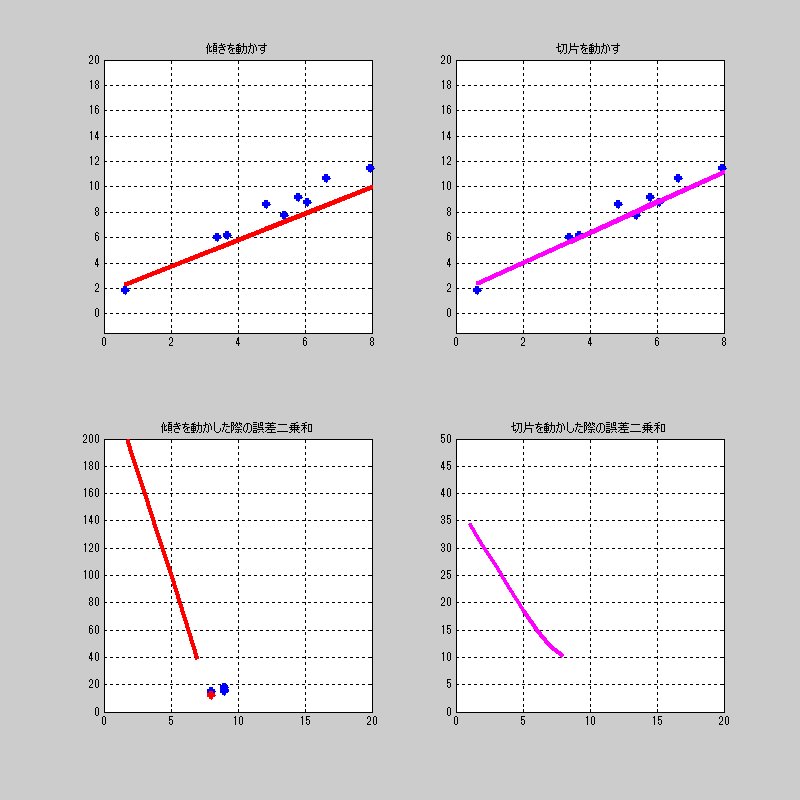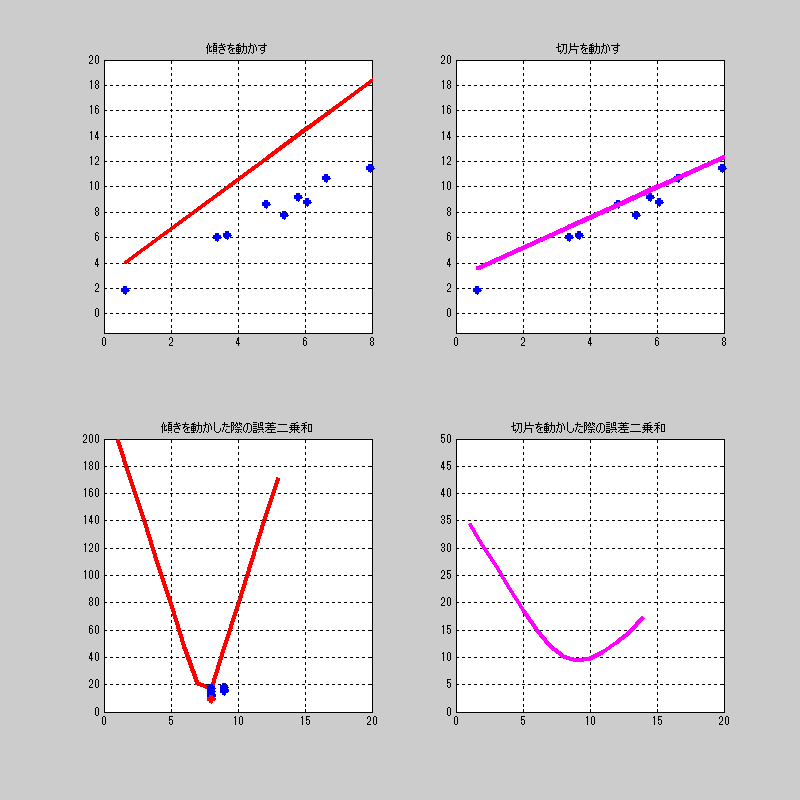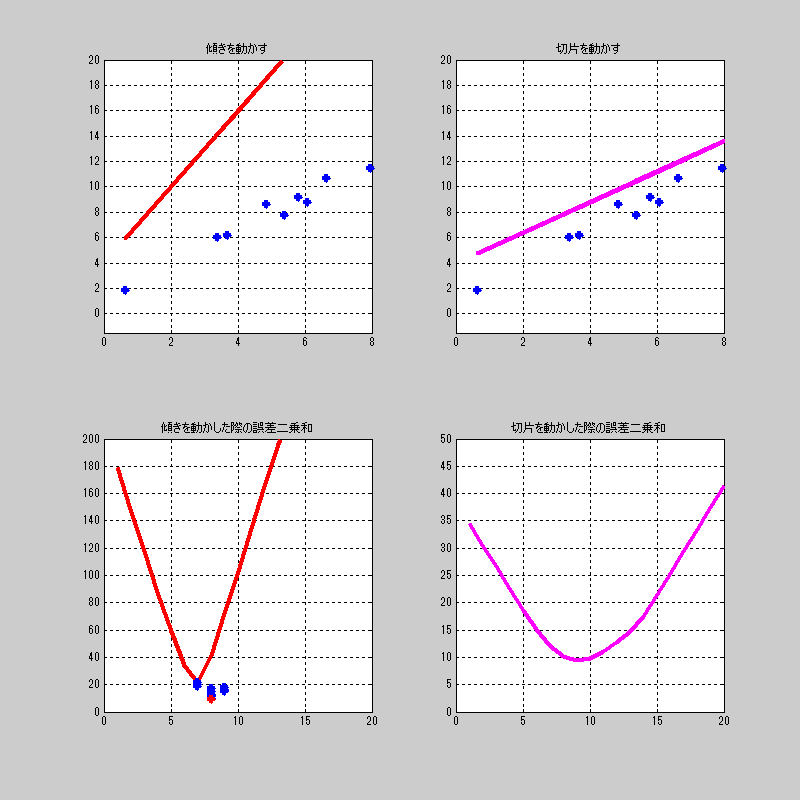
ちなみに、右下の傾きの誤差の最小値に対してプロットするようにしている。
全体を通して、最小値になるプロットだけを赤くしている。
つまり、完全に総当たりを行った後の赤いプロットが求めたい\((a,b)\)がわかる。
しかし、この手法には問題がある。
- 結構時間かかりそう
- \(a\)と\(b\)をちょっとずつ動かしているといっても、その「ちょっと」って適正な値なのか?
総当たりの場合、時間の問題、精度の問題がネックになり、現実的な手法とは言い難い。
これらの問題を回避するために偏微分を利用する。
偏微分は、別に複雑なものではない。
言葉の響きが「変な微分」って聞こえるからアレルギー反応がでるかもしれないが、
どちらかというと、複雑で難しいものを簡単にするためのテクニックになる。
確かにその性質から、「複雑で難しいもの」を対象とするから、その印象で難しいものと認識してしまう人は居るのだろう。





コメント