MATLAB、Scilab、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第2章 その40【二次形式の微分④】
を書き直したもの。
正規方程式を導出するまでの説明。
今回は二次形式の微分(勾配)を実際の多項式に適用したものをMATLABで算出&プロットしてみる。
ロードマップ&数式【再掲】
MATLABで二次形式の微分を確認する。
その前にロードマップを再確認。
二次形式の微分のところになる。

そして、扱う式は以下になる。
\(
f(x,y)=3x^2+2y^2+5xy
\)
二次形式の多項式の偏導関数
\(
\displaystyle\frac{\partial f(x,y)}{\partial x}=6x+5y
\)
\(
\displaystyle\frac{\partial f(x,y)}{\partial y}=4y+5x
\)
二次形式の行列形式の偏導関数
\(
\nabla f(x,y) =
\begin{bmatrix}
\displaystyle\frac{\partial f(x,y)}{\partial x} \\
\displaystyle\frac{\partial f(x,y)}{\partial y}
\end{bmatrix}=
2AX=2
\begin{bmatrix}
3 & 5/2 \\
5/2 & 2
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}
\)
MATLABコード
MATLABコードは以下になる。
a=3;
b=2;
c=5;
A=[a c/2; c/2 b];
N=6;
ax=linspace(0,10,N);
ay=linspace(0,10,N);
[x,y]=meshgrid(ax,ay);
polyY1=6*x+5*y;
polyY2=5*x+4*y;
subplot(2,2,1);
mesh(ax, ay, polyY1);
subplot(2,2,2);
mesh(ax, ay, polyY2);
X=[x(:)';y(:)'];
Y=2*A*X;
matY1=reshape(Y(1,:),N,N);
matY2=reshape(Y(2,:),N,N);
subplot(2,2,3);
mesh(ax, ay, matY1);
subplot(2,2,4);
mesh(ax, ay, matY2);
polyY1
polyY2
matY1
matY2処理結果
そして処理結果。
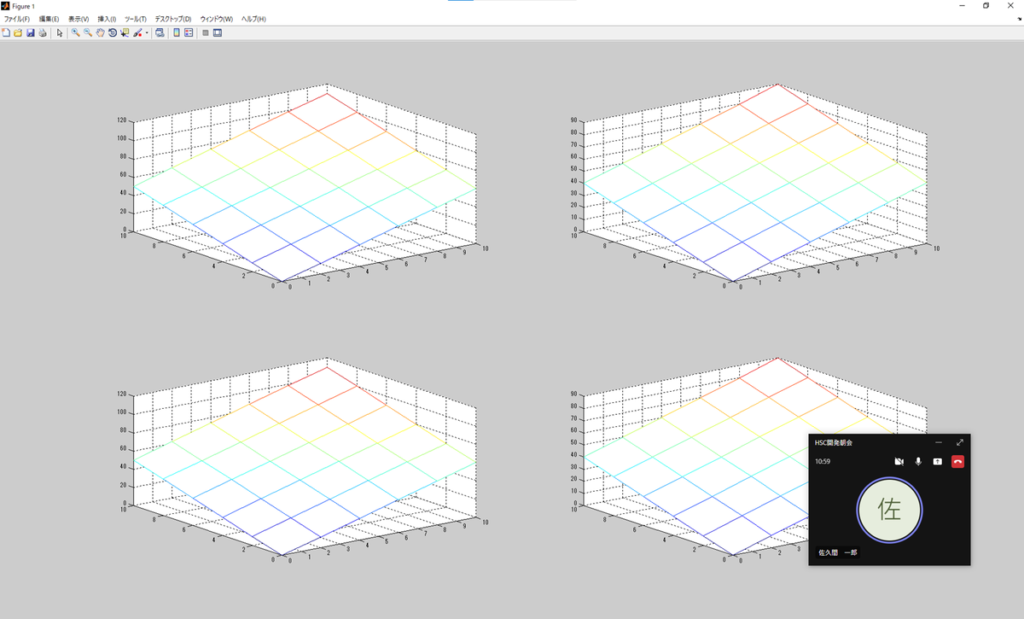
polyY1 =
0 12 24 36 48 60
10 22 34 46 58 70
20 32 44 56 68 80
30 42 54 66 78 90
40 52 64 76 88 100
50 62 74 86 98 110
polyY2 =
0 10 20 30 40 50
8 18 28 38 48 58
16 26 36 46 56 66
24 34 44 54 64 74
32 42 52 62 72 82
40 50 60 70 80 90
matY1 =
0 12 24 36 48 60
10 22 34 46 58 70
20 32 44 56 68 80
30 42 54 66 78 90
40 52 64 76 88 100
50 62 74 86 98 110
matY2 =
0 10 20 30 40 50
8 18 28 38 48 58
16 26 36 46 56 66
24 34 44 54 64 74
32 42 52 62 72 82
40 50 60 70 80 90考察
二次形式の多項式としての偏導関数と行列形式による偏導関数を元にそれぞれを算出及びプロットしてる。
結果としては完全一致。
算出して点としては、それほど多くないが、それぞれの性質の比較としてはOKだろう。
まとめ
- 二次形式の多項式としての偏導関数、行列形式による偏導関数を元にMATLABで算出及びプロット。
- ともに同一の算出結果とプロットが得られた。
MATLAB、Python、Scilab、Julia比較ページはこちら





コメント