tanhを離散的にとらえると?
そして、このtanhの畳み込み積分を離散的にとらえるとどうなるか?
結論としてはシンプル。
引き算をすればOK!
tanhの関数を見るとわかるのだが、
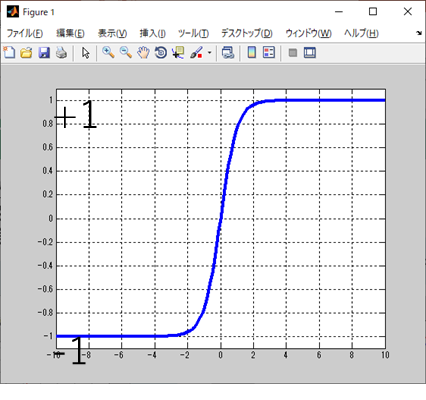
先を+1、あとを-1にしている。
つまり、以下のようなことをするだけでOK

これだけである。
さらに値を顕著にしたい場合
さらに、畳み込みカーネルを工夫することで、変化を顕著に検出することができる。
工夫と言っても+1と-1の間に隙間を入れるだけだが。
図にするとこんな感じになる。

演算結果が大き目で出てるのがわかるだろう。
他もいろいろ
あとは、微分することでエッジ検出できることは良いのだが、
ノイズを大きく拾ってしまう可能性がある。
対策としては、畳み込みカーネルに移動平均的な要素を付加する。
しかし、そうすると元画像の性質が消えやすくなる。
というわけで、ガウシアンカーネル的な特性を付加する。
という感じでどんどんやること、考え事が増えていく…。
まとめると?
やることをまとめると以下4段階になる。
- 微分特性を付けてエッジ検出したい
- 微分の特性をより強くしたい
- 移動平均でノイズをちょっと除去したい
- 元画像の特徴を残すために単純移動平均じゃなくてガウシアンにしたい
このままだと、4つの処理をするイメージになるが、
実際は一つにまとめられる。
つまり、一つの畳み込みカーネルで実現可能。
微分特性を付けてエッジ検出したい
まずは、微分特性を持った畳み込みカーネルの作り方。
これだけでもエッジ検出は可能だ。
\(
K_{dif}=
\begin{bmatrix}
0 \\
1 \\
0 \\
\end{bmatrix}
\begin{bmatrix}
-1 & 1 & 0
\end{bmatrix}=
\begin{bmatrix}
0 & 0 & 0 \\
-1 & 1 & 0 \\
0 & 0 & 0 \\
\end{bmatrix}
\)
この計算の意味がわからないかもしれないが、
「単純に真ん中の”行”に対して、引き算を実施する行ベクトルを入れ込む。」
程度の意味合い。
この書き方は、この後に意味を持ってくる。
微分の特性をより強くしたい
次は、微分の特性を強くしたい。
以下の数式で畳み込みカーネルを導出する。
\(
K_{dif1}=
\begin{bmatrix}
0 \\
1 \\
0 \\
\end{bmatrix}
\begin{bmatrix}
-1 & 0 & 1
\end{bmatrix}=
\begin{bmatrix}
0 & 0 & 0 \\
-1 & 0 & 1 \\
0 & 0 & 0 \\
\end{bmatrix}
\)
わざと隙間を空けて、離れた範囲で差をとっている。
移動平均でノイズをちょっと除去したい
次は移動平均の要素を入れ込む。
ここでは、列方向を移動平均、行方向を微分って考え方になる。
\(
K_{pre}=
\begin{bmatrix}
1 \\
1 \\
1 \\
\end{bmatrix}
\begin{bmatrix}
-1 & 0 & 1
\end{bmatrix}=
\begin{bmatrix}
-1 & 0 & 1 \\
-1 & 0 & 1 \\
-1 & 0 & 1 \\
\end{bmatrix}
\)
元画像の特徴を残すために単純移動平均じゃなくてガウシアンにしたい
最後にガウシアン。
さっきの移動平均を追加したものに対してちょい修正するだけ。
\(
K_{sbl}=
\begin{bmatrix}
1 \\
2 \\
1 \\
\end{bmatrix}
\begin{bmatrix}
-1 & 0 & 1
\end{bmatrix}=
\begin{bmatrix}
-1 & 0 & 1 \\
-2 & 0 & 2 \\
-1 & 0 & 1 \\
\end{bmatrix}
\)
真ん中の行を強くして、結果として元画像の特性が残るようにした。



コメント