MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第3章 その25【微分フィルタ①】
MATLAB,Python,Scilab,Julia比較 第3章 その26【微分フィルタ②】
MATLAB,Python,Scilab,Julia比較 第3章 その27【微分フィルタ③】
MATLAB,Python,Scilab,Julia比較 第3章 その28【微分フィルタ④】
MATLAB,Python,Scilab,Julia比較 第3章 その29【微分フィルタ⑤】
MATLAB,Python,Scilab,Julia比較 第3章 その30【微分フィルタ⑥】
MATLAB,Python,Scilab,Julia比較 第3章 その31【微分フィルタ⑦】
を書き直したもの。
畳み込み演算の微分フィルタの話。
- エッジ検出の雰囲気。
- エッジ検出と微分。
- 微分を離散的に考えると?
- エッジ検出の畳み込みカーネルの方針
- 各種微分フィルタ解説
- Sobelフィルタについて解説。
- Sobelフィルタを実験するための処理を確認。
画像処理と言えば?
前回までで、ガウシアンフィルタってのが終わったところ。
ガウシアンフィルタは、最も基本的な画像処理という位置づけになる。
とはいえ、
ガウシアンフィルタがノイズ除去してくれそうなのはわかったが、
あんまり画像処理って感じがしない。
画像処理と言うと、写真に写ってる物体の輪郭を抽出などの
いわゆるエッジ検出などが思い浮かべやすい。
エッジ検出は一見大変そうな気もするが、それほど大変でもない。
エッジ検出の考え方
まずはエッジ検出を考えるために以下の画像を用意した。
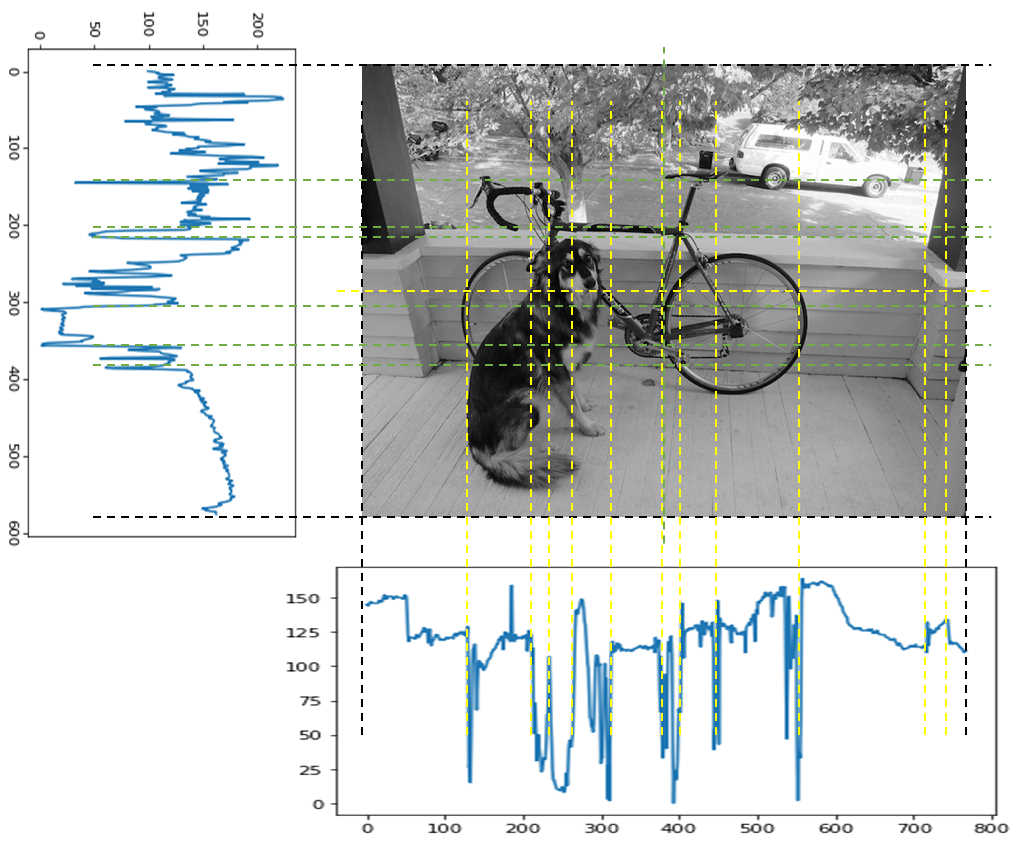
恒例の犬と自転車の画像だが、左と下に謎のグラフが付いている。
これグラフは画像の輝度を示している。
画像自体はグレースケールにしているので、
ピクセルの値が大きいほど、白に近付き、輝度が高いと言える。
そして、その輝度に山と谷があることがグラフから読み取れる。
そして、輝度の立ち上がり、立下りが激しい部分を実際の画像と見比べると、
何かしらの物体の境界線になっていることが多い。
つまり、この山と谷を検知すれば、結果的にエッジ検知になる。
って寸法。
この山と谷の検知、普通に考えると、ピクセル同士を比較するようなプログラムが最初に頭に浮かぶと思う。
当然、それでも実現可能ではあるが、if文だらけの見通しのよろしくないプログラムになりそうだ。
実は、エッジ検出にif文はほぼ不要。(for文は使うが)
エッジ検出するためには?
エッジを検出する方法で、if文の嵐なプログラム以外にどう解決するのか?
要は、山と谷がある部分が協調されれば良い。
山と谷は変化の激しい部分だ。
変化が激しいと値が大きくなる計算方法がある。
さて、これは何だろうか?
答えは微分。
簡単に微分っぽいことを実現するには?
微分というと導関数を求めるイメージがあるかもしれないが、
任意の画像の導関数を求めるの現実出来ではない。
今回の目的は、輝度の山と谷を知りたいだけ。
よって、単純に値の差が求まればOK。
完璧な微分を実施する必要はない。
微分と同じ効能が得られる演算をすればOK。
微分と同じ効能を得られる演算だが、
具体的には、
「tanh関数で畳み込み積分をする。」
になる。
微分なのに積分?
と思うかもしれないが、tanh関数で畳み込むと微分相当の結果になる。
tanh関数は、「ハイパボリックタンジェント」と言って、
こんな関数になる。
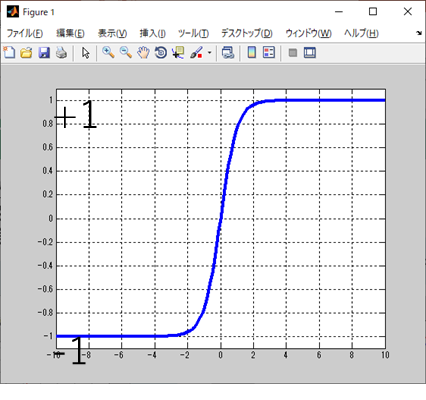
ニューラルネットワークの活性化関数とかで見たことある人もいるだろう。
tanh関数を使って畳み込み積分
このtanh関数を使って畳み込み積分をするとこうなる。
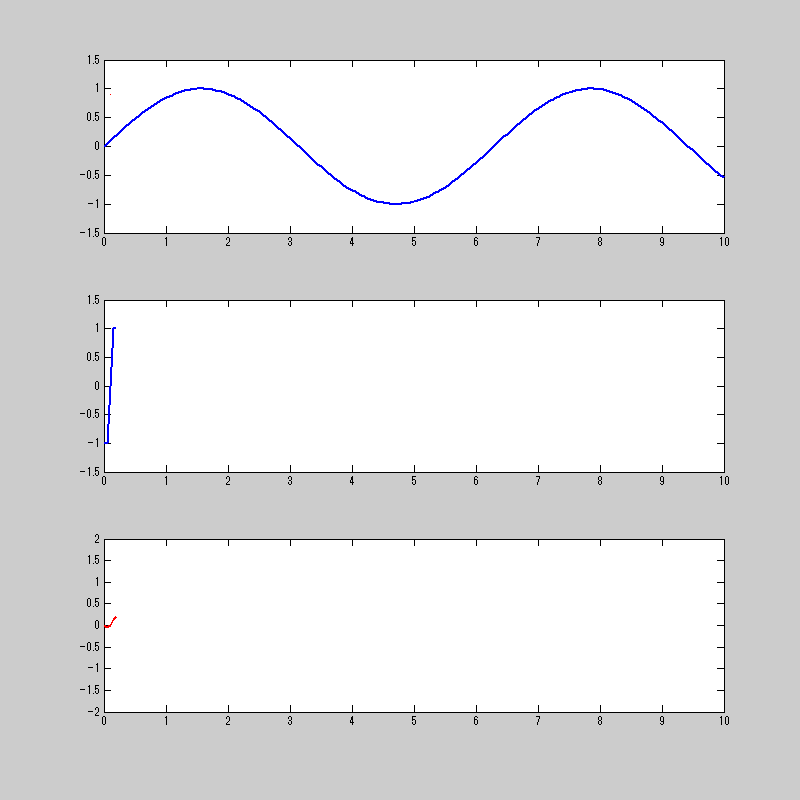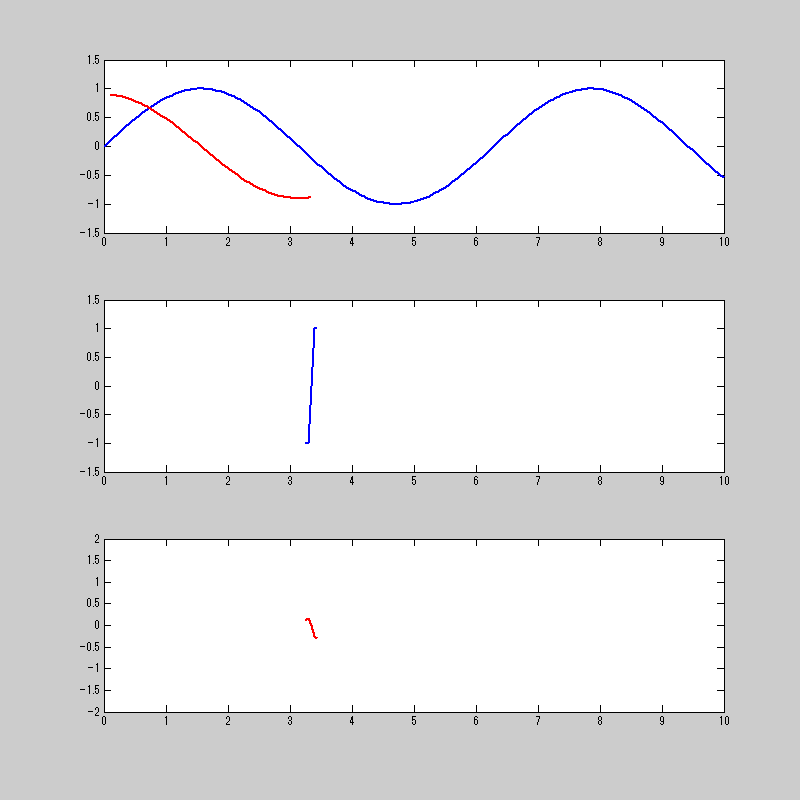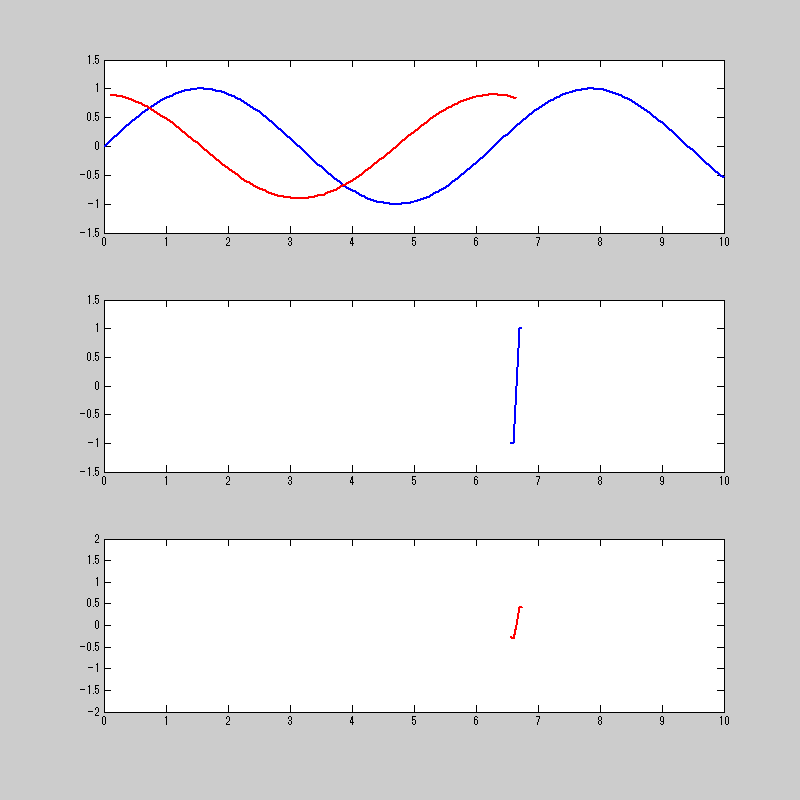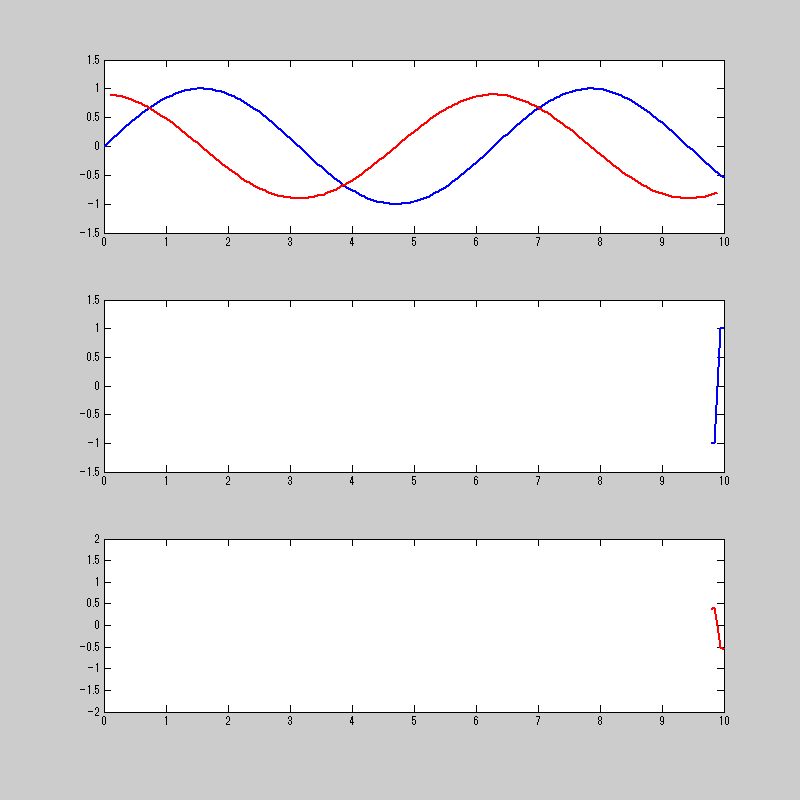
sin関数がcos関数になってるから、微分ができてると言って良いだろう。
注意点としては、あくまで微分相当であり、微分そのものではないってところ。
先のgif画像は、微分っぽさを強調するため、畳み込みの結果にある程度のゲインを掛けてる。
欲しいのは、微分の変化が大きい部分を強調という性質なので、これでも十分と言える。
発想としては微分なんだけど、微分そのものじゃなくて、強調できる機能が欲しいってだけなので。
あとは、これを離散的に解釈した場合とか、画像のような平面に適用する場合にどうするかを考える。





コメント