はじめに
※ 本記事は以下を親記事とした子記事に該当する。
https://www.simulationroom999.com/blog/mechanics-overview/
まずは加速度の話から。
加速度は”力”を表現する上で最も重要な概念となる。
加速度とは
加速度(かそくど、英: acceleration)は、単位時間当たりの速度の変化率。速度ベクトルの時間的な変化を示すベクトルとして加速度が定義される。
Wikipediaより


要は、速度の変化量を加速度と呼ぶ。
問題は、加速度そのものは人間が見ることはでいない。
よって、定義が必要となる。
加速度そのものの定義よりも、加速度を使用した、速度\([m/sec]\)と距離\([m]\)の定義が重要となる。
速度と距離の定義
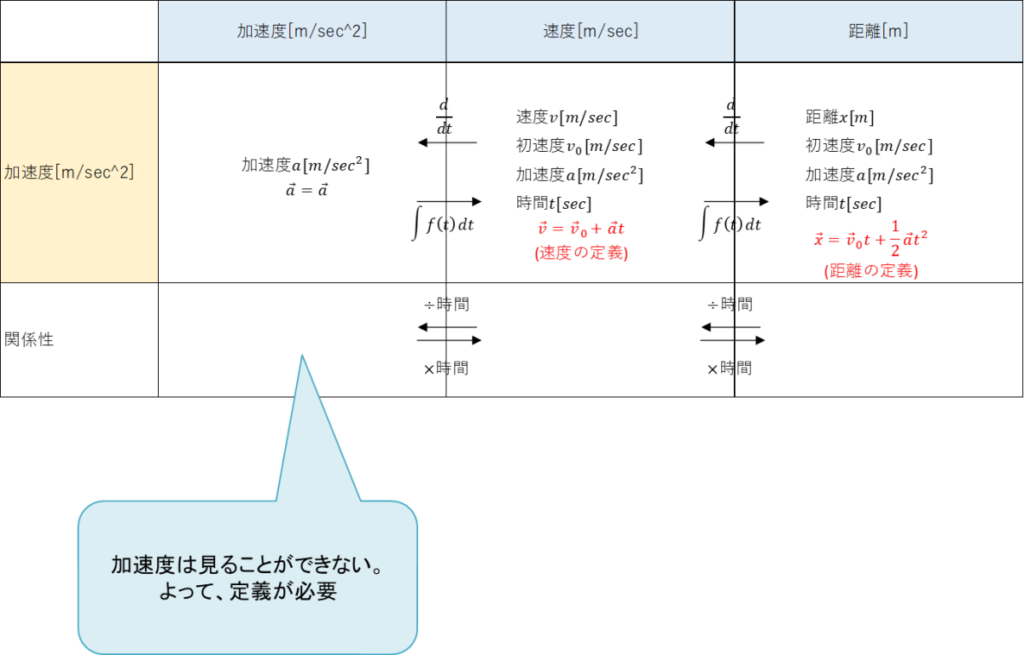
極論、上記の表だけ覚えて、以下は読まなくても良い。
速度の定義
速度\(v[m/sec]\)
初速度\(v_0[m/sec]\)
加速度\(a[m/sec^2]\)
時間\(t[sec]\)
加速度は速度の変化量であることから、
$$\vec{v(t)}\frac{d}{dt}=\vec{a}$$
両辺をtで積分。
$$\vec{v(t)}=\int \vec{a(t)}dt+C$$
上記を一般解から特殊解に。
初期条件:\(\vec{v}(0)=\vec{v_0}\)
要は、初速度を決めておく程度の話。
$$\vec{v(t)}=\int \vec{a(t)}dt+\vec{v_0}$$
\(\vec{a(t)}\)が変化しないことを前提とすると、積分を掛け算に置き換えできる。
$$\vec{v}=\vec{a}t+\vec{v_0}$$
これが加速度を使用した速度の定義となる。
要は、
初速度に、加速度×時間を足すと現在の速度になる。
距離の定義
距離\(x[m]\)
初速度\(v_0[m/sec]\)
加速度\(a[m/sec^2]\)
時間\(t\)
速度は、移動距離の変化量である。
よって、
$$\vec{x(t)}\frac{d}{dt}=\vec{v(t)}$$
両辺を積分する。
$$\vec{x(t)}=\int \vec{v(t)} dt$$
\(\vec{v}\)を加速度\(\vec{a}\)の表現に置き換える
$$\vec{x}=\int (\vec{a}t+\vec{v_0})dt$$
積分を解く。
$$\vec{x(t)}=\frac{1}{2}\vec{a}t^2+\vec{v_0}t$$
これが加速度を使用した距離の定義となる。
距離は以下の2つの表現方法が可能。
- 距離は加速度を2階積分したもの
- 速度を1階積分したもの
まとめ
- 加速度と力は密接な関係にある。
- しかし、加速度は人間が見ることができない。
- よって、速度、距離を利用した定義が必要。
- 加速度という概念を用いて、速度と距離を定義することで加速度を定義している。
大学入試 漆原晃の 物理基礎・物理[力学・熱力学編]が面白いほどわかる本
大人のための高校物理復習帳 役立つ物理の公式28 (ブルーバックス)
はじめて学ぶ物理学—学問としての高校物理(上)
はじめて学ぶ物理学—学問としての高校物理(下)




コメント