MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その85【複素フーリエ係数⑩】
MATLAB,Python,Scilab,Julia比較 第5章 その86【複素フーリエ係数⑪】
を書き直したもの。
複素フーリエ係数のシリーズ。
前回は複素フーリエ係数の式を導出した。
今回は\(C_0\)について少し言及する。
【再掲】複素フーリエ係数に至る道
まずは複素フーリエ係数に至る道を再掲。
- 複素指数関数の積
- 複素指数関数が直交していない状態
- 複素指数関数が直交している状態
- 複素指数関数の直交性の確認
- 複素フーリエ係数の導出
今回は\(C_0\)について少し言及する。
複素フーリエ係数C0について
\(C_0\)について言及だが、求め方が違うのか?
実は求め方は一緒で、
前回の式を使用すれば勝手求められる。
しかし、少し求められたものの性格が違うので言及しておこうってわけになる。
求められるけど、概念的な違いがあるって感じ。
C0を求めてみる
まずは複素フーリエ係数の式を使用して\(C_0\)を求めてみよう。
\(
\begin{eqnarray}
\displaystyle \int_{-\pi}^{\pi}f(x)e^{-i0x}\,dx&=&\int_{-\pi}^\pi C_0 e^{-i0x}\,dx+\dots\\
&=&\int_{-\pi}^\pi C_0 e^0 e^{-i0x}\,dx\\
&=&\int_{-\pi}^\pi C_0\cdot 1 \cdot 1\,dx\\
&=&2\pi C_0\\
\therefore C_0&=&\frac{1}{2\pi}\int_{-\pi}^\pi f(x)\,dx
\end{eqnarray}
\)
なんかそれっぽい数式が出てきたが、
何を示しているかが分かりにくい。
端的に言うと\(f(x)\)平均になる。
「なんで!?」と思うかもしれなないが・・・。
C0の式を図で見た場合
まず先ほどの式の中の、以下の部分。
\(
\displaystyle\int_{-\pi}^\pi C_0\cdot 1 \cdot 1\,dx\\
\)
ここから、\(2\pi C_0\)になってるところがわからと思う。
が、
図で見たら一発で分かるだろう。
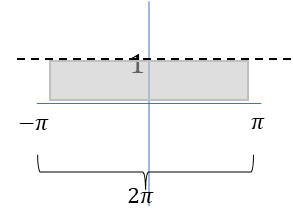
これは以前見せた図でもある。
長方形で考えると良いパターン。
よって、\(2\pi C_0\)になる。
C0が平均な訳
そして、平均だと言ってた式がこれ。
\(
\displaystyle C_0=\frac{1}{2\pi}\int_{-\pi}^\pi f(x)\,dx
\)
普通、平均ってこういう式の方を思い浮かべると思う。
\(
\displaystyle \frac{1}{N}\sum_{i=0}^N
\)
その認識はただしい。
ただし、この式は離散的な関数に於ける平均になる。
そうすると、連続的な関数に於ける平均があるってことになる・・・。
先ほどの離散的な平均との兼ね合いも含めて表現すると以下になる。
\(
\displaystyle \lim_{N\to\infty}{\color{red}{\frac{1}{N}\sum_{i=0}^N F_i}} \Delta x=\frac{1}{N}\int_0^Lf(x)\,dx\dots(N=L/\Delta x)
\)
ちなみに赤文字で示した範囲が一般的というか離散的な関数の平均。
連続的のため、総和じゃなくて、積分を使用する。
結局C0って何者?
\(C_0\)が平均というのは分かったと思うが、
なんで平均がフーリエ係数に紛れてくるんだろうか?
平均と言うと伝わりにくいが、
オフセットと言ったら伝わるかもしれない。
例えば、以下のように連続関数と平均ことオフセットの\(C_0\)を関係を示そう。
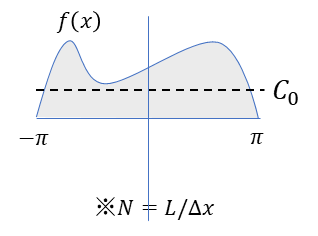
連続関数\(f\)は必ずしも0を中心に動いているわけでは無い。
対して、フーリエ級数の元となっている三角関数は0を中心となっており、
オフセットの表現ができない。
このため別途オフセットに相当する係数が必要になる。
それが\(C_0\)の位置づけとなる。
まとめ
- フーリエ係数のC0について言及。
- 結果としてC0は関数f(x)の平均値を示す。
- 離散関数の平均と連続関数の平均の関係性。
- 結局C0は三角関数では表現できない関数のオフセット成分となる。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす





コメント