MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その92【複素フーリエ係数(周期2L)①】
MATLAB,Python,Scilab,Julia比較 第5章 その93【複素フーリエ係数(周期2L)②】
を書き直したもの。
前回までで複素フーリエの話がおおよそ終わったところだが、
実数フーリエの時と同様に周期が2π限定になっているため、
周期を任意にできるようにする必要がある。
というわけで、周期2πから周期2Lへ置き換えをする。
任意周期
とりあえず複素フーリエも完了・・・。
と思いきや、まだちょっとある、
現状の複素フーリエは、周期が\(2\pi\)が前提になってしまっている。
(実数フーリエの時も同じ話があった。)
というわけで、複素フーリエも任意周期に対応させる。
周期2L
複素フーリエの任意周期化も実数フーリエと同じアプローチになる。
\(2\pi\)を\(2L\)に置き換えるって感じになる。
画像で示すと以下になる。
実数フーリエの時と同じもの。
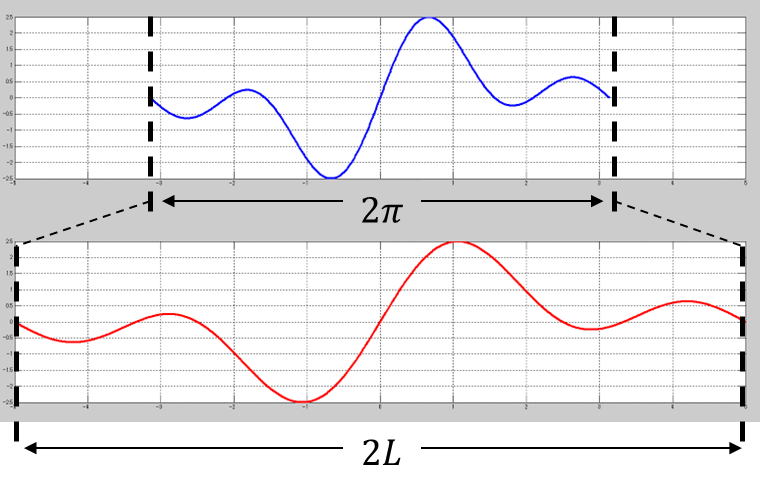
ちなみに、0を中心とした\(2\pi\)の範囲の線対称は、cos関数の影響だな。
sin関数は奇関数なので0中心であれば、積分時に必ず0になるが、
cos関数の方は偶関数のため、\(2\pi\)の範囲でないと積分時に0にならない、
これは直交性に影響する話になる。
ここは実数フーリエの時にも言ってた。
複素フーリエでは複素指数関数ではあるが、
オイラーの公式から、結局はcos関数とsin関数の組み合わせであることは変わらないため、同じ理屈になる。
【再掲】複素フーリエ
ここから複素フーリエの任意周期化。
まずは、複素フーリエ級数と複素フーリエ係数を再掲しておこう。
複素フーリエ級数
\(
\displaystyle f(x)=\sum_{n=-\infty}^{\infty}C_n e^{inx}
\)
複素フーリエ級数
\(
\displaystyle C_n=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)e^{-inx}\,dx
\)
横軸を置き換え
実数フーリエの時と同じだが、
\(2\pi\)を\(2L\)に変換する式を導出する。
\(
\begin{eqnarray}
\displaystyle x&=&\frac{2L}{2\pi}t=\frac{L}{\pi}t\\
\therefore t&=&\frac{\pi}{L}x
\end{eqnarray}
\)
よって、周期を\(2L\)に解釈し直した複素フーリエ級数は以下になる。
\(
\displaystyle f(x)=\sum_{n=-\infty}^{\infty}C_n e^{i\frac{n\pi x}{L}}
\)
同じように、周期を\(2L\)に解釈し直した複素フーリエ係数は以下となる。
\(
\displaystyle C_n=\frac{1}{2L}\int_{-L}^{L}f(x)e^{-i\frac{n\pi x}{L}}\,dx
\)
流れとしては実数フーリエの時と全く一緒か。
実数フーリエの段階でやってたことなため、
複素フーリエになってもすんなりと入ってくるだろう。
まとめ
- 前回までの複素フーリエは、周期が2πという制約がある。
- 2πを2Lに変換することで任意周期に対応させる。
- このアプローチは実数フーリエの時と同じ。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす





コメント