MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その77【複素フーリエ係数②】
MATLAB,Python,Scilab,Julia比較 第5章 その78【複素フーリエ係数③】
を書き直したもの。
前回から複素フーリエ係数のシリーズに突入。
今回は「複素指数関数が直交していない状態」「複素指数関数が直交している状態」を確認。
【再掲】複素フーリエ係数に至る道
まずは複素フーリエ係数に至る道を再掲。
- 複素指数関数の積
- 複素指数関数が直交していない状態
- 複素指数関数が直交している状態
- 複素指数関数の直交性の確認
- 複素フーリエ係数の導出
今回は「複素指数関数が直交していない状態」「複素指数関数が直交している状態」を確認する。
複素指数関数同士の積の積分
まず、前回の指数関数の性質の式を再掲しておく。
\(
e^{imx}e^{-inx}=e^{m-n}x
\)
そして、以下の積分について考える。
\(
\displaystyle \int_{-\pi}^{\pi}e^{imx}e^{-inx}dx=\int_{-\pi}^{\pi}e^{i(m-n)x}dx
\)
指数関数の性質を考えると一つの指数関数にまとめられる。
これが複素フーリエ係数に繋がる式でもある。
複素指数関数が直交していない状態
そして、先ほどの式を評価することで直交評価ができる。
実数フーリエの時の三角関数同士の評価と同じと言える。
関数を無限次元ベクトルと解釈すると内積と同じになり、
0であれば直交、0でなければ直交していない。
まずはわかりやすい直交していない場合を考える。
答えとしては\(m=n\)の時は直交していないと言える。
代入した結果は以下になる。
\(
\begin{eqnarray}
\displaystyle \int_{-\pi}^{\pi}e^{i(m-m)x}dx&=&\int_{-\pi}^{\pi}e^0 dx\\
&=&\int_{-\pi}^{\pi}1\,\,dx\\
&=&2\pi
\end{eqnarray}
\)
指数部が0だと1になるのは分かるが、
積分の結果が\(2\pi\)になる理由がわからないという人がいるかもしれない。
これは積分の範囲が\(-\pi\sim\pi\)の\(2\pi\)の範囲だから。
以下の図をイメージしてもらうと分かると思う。
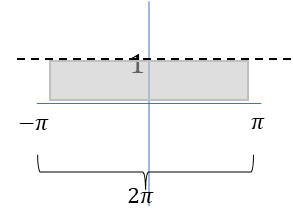
\(2\pi\times 1\)の長方形の面積になるから\(2\pi\)ってことになる。
そして、内積の結果として0にならないことが証明された。
つまり、n=mの時は直交しない。
直交している場合
そうすると、今度はm≠nのパターンで、
直交しているかどうかを確認になる。
早速確認してみよう。
\(
\begin{eqnarray}
\displaystyle \int_{-\pi}^{\pi}e^{i(m-n)x}dx&=&\frac{1}{i(m-n)}\Big[e^{i(m-n)x}\Big]_{-\pi}^{\pi}\\
&=&\frac{1}{i(m-n)}(e^{i(m-n)\pi}-e^{-i(m-n)\pi})
\end{eqnarray}
\)
ここでオイラーの公式とその変形式を利用する。
\(
\begin{eqnarray}
e^{in\pi}=\cos(n\pi)+i\sin(n\pi)\\
e^{-in\pi}=\cos(n\pi)-i\sin(n\pi)\\
\end{eqnarray}
\)
\(n\)は整数が入るため、\(n\pi\)は\(\pi\)の倍数となる。
この場合、
\(\sin(n\pi)\)は必ず0となる。
つまり虚数部は必ず0となる。
\(\cos(n\pi)\)は\((-1)^n\)となる。
よって、以下に整理できる。
\(
\begin{eqnarray}
e^i{m-n}\pi-e^{i(m-n)\pi}&=&(-1)^{m-n}-(-1)^{m-n}=0\\
\therefore\int_{-\pi}^{\pi}e^{i(m-n)x}x&=&0
\end{eqnarray}
\)
0になった。
と言うことは内積が0ということで、
n≠mの時は直交していることになる。
まとめ
- 複素指数関数同士の積の積分の式を提示。
- 複素指数関数でn=mの時は直交しない。
- 結論としてはn≠mの時に直交する。
- これらはオイラーの公式と三角関数の性格から特定ができる。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす





コメント