それぞれの関数の確認
とりあえず、各関数が奇関数か偶関数か特定できたところ。
以下の感じになる。
- \(x^3\)は奇関数
- \(\cos(2x)\)は偶関数
- \(\sqrt{4-x^2}\)は半円の方程式なので偶関数(半円なのでy軸に対して線対称)
偶関数、奇関数の特性を利用して解く
奇関数と偶関数を掛けたものは奇関数のため、
\(x^3\cos(2x)\sqrt{4-x^2}\)は
奇関数×偶関数×偶関数=奇関数
そして、奇関数を-2から2の範囲の定積分を行うと必ず0になる。
つまり、この式になる。
\(
\displaystyle\int_{-2}^2\frac{1}{2}\sqrt{4-x^2}dx\\
\)
さらに、\(\sqrt{4-x^2}\)は偶関数なので、
0から2の定積分の2倍したものと等しくなる。
\(
\begin{eqnarray}
&&2\displaystyle\int_{0}^2\frac{1}{2}\sqrt{4-x^2}dx\\
&=&\displaystyle\int_{0}^2\sqrt{2^2-x^2}dx
\end{eqnarray}
\)
偶関数の特性を利用して解く
これが四分円の面積になるのだが、
図として示した方が分かりやすいだろう。
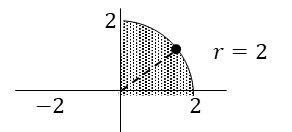
半径2の円を4分の1にしたものになる。
そうすると以下で解ける。
\(
\displaystyle\frac{\pi r^2}{4}=\frac{4\pi}{4}=\pi
\)
という感じで答えは\(\pi\)になる。
\(\pi\)なんてどこにも出てこなかったものが答えなるのは不思議と思うかもしれない。
半円の方程式が隠れており、
\(\pi\)はそこからの由来となる。
\(x^3\cos(2x)\)の方は奇関数であるが故に消えちゃう部分なので無関係の部分となる。
まとめ
- 前回の数学パズルを真面目に解いてみる。
- まずは平方根の関数の正体を探る。
- 偶関数、奇関数の特性を利用しまくって定積分を最適化しまくる。
- ほとんどが0に消えて、半円の方程式だけが残る。
- さらに偶関数の特性を利用して四分円にする。
- 半径2の円を四等分すれば答えが出る。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント