OpenCVによる画像処理入門
画像処理概要
- 画像の読み込み、保存について具体的にやることを列挙。
- カメラキャプチャもやるが、ツール、言語によってはできないor難しい場合あり。
- 使用する画像は例の「犬と自転車」。
- お試し画像処理は赤成分の抽出と左右反転をやってみる。
MATLAB
MATLABではImage Processing Toolboxが必要。
なのだが、標準機能で頑張って画像処理をしてみた。
- MATLABで画像処理。
- 読み込みはimread。
- 画像の構成を維持した2次元配列に、RGBの3チャンネルがぶら下がる。
- 結果として3次元配列になる。
- 画像の構成を維持した2次元配列に、RGBの3チャンネルがぶら下がる。
- 画像の加工は配列操作を駆使する。
- 配列操作の基本を身に着けた方がお得。
詳解 OpenCV 3 ―コンピュータビジョンライブラリを使った画像処理・認識
Python
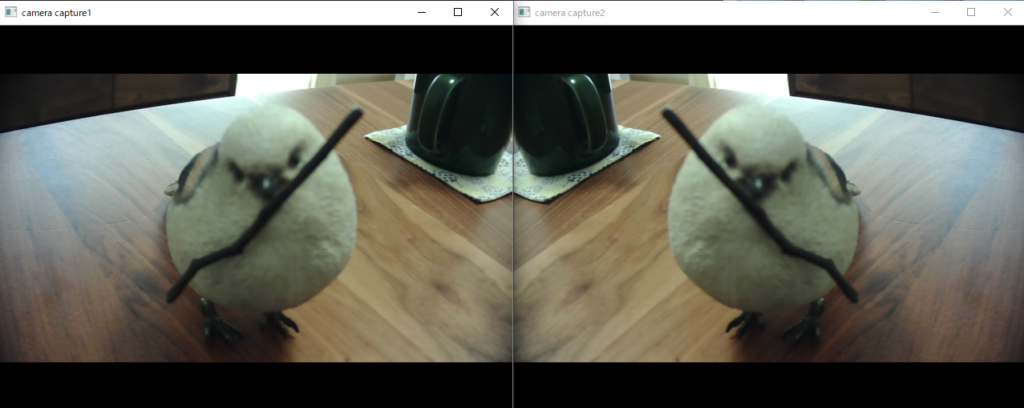
Scilab
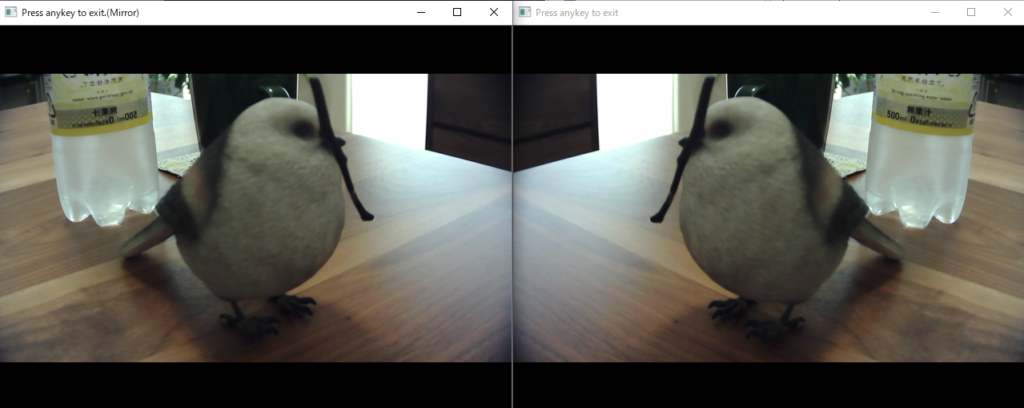
Julia
- Juliaで画像処理。
- ImagesとImageViewのパッケージをインストール。
- OpenCVではなくImageMagickを使用したパッケージなので他の環境と性格が異なる。
- ImagesのAPIとやり取りする場合は基本構造体ベースだが、処理をする際は配列にするなど行ったり来たりが発生する。
グレースケール
- 画像処理の実験をする際はグレースケールにしておくのが一般的。
- グレースケールにも種類がある。
- 犬と自転車の画像を元にRGB平均とSDTV規格を比較してみた。
- 今後の予定としては各ツール、各言語でこれらを実施し、クセのようなものを認識する。
MATLAB
- MATLABでRGB平均とSDTVのグレースケール化実施。
- 画像データの型の都合でuint8のキャストが必要。
- unit8キャスト時に小数点以下が自動で四捨五入される。
- 小数点以下切り捨て(0方向への丸め)をしたい場合はfix関数を使用する。
Python
- Python(NumPy)でRGB平均とSDTVのグレースケール化実施。
- 次いでにOpenCVによるグレースケール化も。
- OpenCVによるグレースケール化はコーデック依存な面がある。
- 画像データはの1チャンネル1ピクセルは8bit長。
Scilab
- ScilabでRGB平均とSDTVのグレースケール化実施。
- 基本的にはMATLABと似た感じにはなる。
- デフォルトで0方向へ丸め。
- 整数型でキャストすると内部の変数も演算前に整数型に変わってしまう。
- これを抑制するためにdoubleへキャストなどを使用する。
Julia
- JuliaでRGB平均とSDTVのグレースケール化実施。
- 基本的な流れは他の環境と一緒。
- データ構造の違いに気を付ける必要がある。
- さらに各チャンネル情報も0~1の正規化されたものになってる点にも注意。
ガウシアンフィルタ
- ガウシアンフィルタについて説明。
- 畳み込み演算、畳み込み積分。
- 2次ガウス分布関数と近似の良く使われる2次ガウス分布カーネル。
- 実際に試す際は畳み込み演算の関数を作成予定。
MATLAB
- MATLABでガウシアンフィルタを実施。
- 畳み込み演算は関数化。
- MATLABのsumは行と列のそれぞれの総和しか計算できない。(version依存)
- RGB 3chに対して同じ処理を実施している。
Python
- Python(NumPy)でガウシアンフィルタを実施。
- 畳み込み演算は関数化。
- NumPyのsumは行列の総和。
- 行、列の総和の場合はaxisオプションを使用。
- RGB 3chに対して同じ処理を実施。
Scilab
- Scilabでガウシアンフィルタを実施。
- 畳み込み演算は関数化。
- Scialbのsumは行列の総和。
- 行、列の総和の場合は第2引数を使用。
- RGB 3chに対して同じ処理を実施。
Julia
- Juliaでガウシアンフィルタを実施。
- 畳み込み演算は関数化。
- Juliaのsumは行列の総和。
- 行、列の総和の場合はdimsオプションを使用。
- RGB 3chに対して同じ処理を実施。
- データ構造が大きく異なるので注意。
微分フィルタ
- エッジ検出について説明。
- 各種微分フィルタについて説明。
- Sobelフィルタを元にいろいろ課題認識&対策実施。
- 実験手順を説明。
MATLAB
- MATLABでSobelフィルタを実施。
- 想定通りの結果が得られた。
- というより、前回までの結果が実はMATLABで実施したものだった。
- 他の環境、言語でも同様の結果が得られるかが確認ポイントになる。
Python
- Python(NumPy)でSobelフィルタを実施。
- MATLABと同じ結果が得られた。
- np.arrayがuint8になっている状態を維持する必要がある。
- imwrite時にuint8になっていないと期待した出力にならない。
Scilab
- ScilabでSobelフィルタを実施。
- MATLABと同じ結果が得られた。
- uint8にキャストする際は、事前にmin,maxを使用してサチュレーションをしておく必要がある。
Julia
- JuliaでSobelフィルタを実施。
- MATLABと同じ結果が得られた。
- コード上の演算はほぼMATLABと一緒
- 画像が0~1で正規化されている点に注意。
- 画像書き出し時にも再度正規化しておくと良い。
非極大値抑制
- 非極大値抑制(Non-maximum suppression)について説明。
- 概念としてはシンプルだが、2次元平面で考える場合、どの方向から極大値を評価するが重要。
- x方向、y方向の輝度勾配が分かっているので、勾配の方向はarctanで特定可能。
MATLAB
- MATLABで非極大値抑制を実施。
- 想定通りの結果が得られた。
- 論理インデックスサーチを利用している個所がある。
- インデックスサーチについては別途説明。

【入門】非極大値抑制(MATLAB)【数値計算】
MATLABで非極大値抑制を実施。
想定通りの結果が得られた。
論理インデックスサーチを利用している個所がある。
インデックスサーチについては別途説明。
Python
- Python(NumPy)で非極大値抑制を実施。
- MATLABと同一の結果が得られた。
- MATLABでは論理インデックスサーチを使用したが、ここではあえて線形インデックスサーチを使用。
Scilab
- Scilabで非極大値抑制を実施。
- MATLABと同様の結果が得られた。
- コードもほぼ一緒。
- Scilabも線形&論理インデックスサーチが存在する。
Julia
- Juliaで非極大値抑制を実施。
- MATLABと同様の結果が得られた。
- ピクセルの正規化の話と、”.”によるブロードキャストは毎度な話。
インデックスサーチ
- MATLABで線形インデックスサーチと論理インデックスサーチの挙動を確認。
- 基本的な考え方は配列の添え字指定のベクトル化。
- 線形の場合は、要素番号、論理の場合は、0or1のテーブル指定。
- 各ツール、各言語で線形インデックスサーチを確認。
- 基本的にはどの環境でも実施可能。
- MATLABのfind相当の関数がwhereだったりfindallだったりする程度の差はある。
- 各ツール、各言語で論理インデックスサーチを実施。
- 基本的には似たり寄ったりの記述方法。
- 各ツール、各言語における論理インデックスサーチと線形インデックスサートの一覧表を作成。
- SQLやコンテナライブラリにも似たような機能が実装されていることが多いので、仕様を確認しておくと楽ができる。
Hysteresis Threshold
- 2値化手法として、Hysteresis Thresholdを使ってみる。
- Hysteresis Thresholdを図解&判定方法を説明。
- Hysteresis Thresholdを実施するための手順を確認。
MATLAB
- 非極大値抑制にHysteresis Thresholdを加えた、Canny法による2値化をMATLABで実施。
- 基本的にはいままでのコードを再利用。
- 追加分はHysteresis Thresholdの部分。
Python
- 非極大値抑制にHysteresis Thresholdを加えた、Canny法による2値化をPython(NumPy)で実施。
- 基本的にはいままでのコードを再利用。
- 追加分はHysteresis Thresholdの部分。
Scilab
- 非極大値抑制にHysteresis Thresholdを加えた、Canny法による2値化をScilabで実施。
- 基本的にはいままでのコードを再利用。
- 環境によってはメモリ不足に陥るのでJavaヒープメモリを調整する必要がある。
Julia
- 非極大値抑制にHysteresis Thresholdを加えた、Canny法による2値化をJuliaで実施。
- 環境依存はあるかもしれないが、処理としてはMATLABよりも高速。
- JITコンパイル後はネイティブコードで動作するため。
アフィン変換
- 座標変換の代表的な手法としてアフィン変換がある。
- アニメーションgifでアフィン変換のイメージを見てみた。
- アフィン変換を実施する上での問題を確認。
- 空間不足問題とまだら模様問題。
アフィン変換実験前のキャンバス拡張
MATLAB
- キャンパス拡張をMATLABで実施。
- 元画像のサイズを元に指定ピクセル分大き目の黒空間を作成。
- その黒空間の真ん中に元画像をコピー。
Python
- キャンパス拡張をPython(NumPy)で実施。
- 手順としてはMATLABと一緒。
- 黒空間を作る際にuint8の型で作成。
- 保存時にキャストしてもOK。
Scilab
- キャンパス拡張をScilabで実施。
- 手順としてはMATLABと一緒。
- メモリ不足になることがあるため、画像を小さめにしておいた方が良い。
Julia
- キャンパス拡張をJuliaで実施。
- 手順としてはMATLABと一緒。
- だいたい0~1の正規化が他のツール、言語の差異になりやすいが、今回は関係ない。
アフィン変換と畳み込みニューラルネットワーク
- 余談として畳み込みニューラルネットワークと畳み込み演算、アフィン変換の関連性を説明。
- 畳み込み層と畳み込み演算は割とそのまんまでわかりやすい。
- アフィン変換の同次座標系の全結合層の数式を比較。
- 全結合層は別名でアフィン層。
アフィン変換まだら模様対策
- アフィン変換後にまだら模様になる問題がある。
- まだら模様対策のシンプルなやつを確認。
- アフィン逆変換を使う。
- アフィン逆変換は、アフィン変換の式を変形しただけ。
- アフィン行列が逆行列になる。
アフィン変換とアフィン行列
- 各種アフィン変換とアフィン行列の説明。
- 回転行列について説明。
- 動く点Pで回転移動の雰囲気を察する。
- cos,sinを使って直交座標へ。
- 基本ベクトルの変化を元に回転のイメージを得る。
- x軸、y軸の回転を合わせて行列へ。
アフィン変換のプログラミングに向けて
- アフィン変換のプログラムの流れを確認。
- 中心を0とした座標系。
- アフィン変換を一括で行うための変形。
- 元の座標系の戻す。
- 元画像と変換元座標を元に変換先へコピー。
MATLAB
- MATLABでアフィン変換の伸縮を実施。
- 問題無く動作。
- 他のアフィン変換も動くはずだが、別途実験予定。
MATLAB
- Python(NumPy)でアフィン変換の伸縮を実施。
- 問題無く動作。
- 配列の次元の辻褄あわせのためリストのアンパック仕様を利用している。
- no.blockなどの行列結合でもOK。
Scilab
- Scilabでアフィン変換の伸縮を実施。
- 問題無く動作。
- 環境によってはメモリ不足問題が起きる。
- 画像サイズを小さくするなどで対応が必要。
Julia
- Juliaでアフィン変換の伸縮を実施。
- 問題無く動作。
- meshgridが無いので該当関数を自作。
アフィン行列の合成
- アフィン行列の合成できる。
- 行列の結合法則について説明。
- 行列の結合法則を証明。
- 上記により、アフィン行列の合成が証明される。
- アフィン逆行列のアルゴリズムを使用している都合、逆行列の結合法則にも気を付ける必要がある。
- 「行列の積の逆行列」と「逆行列の積」の関係性を証明。
- 上記を利用して、アフィン逆変換の合成を各アフィン行列単体で管理できる形状に変形。
MATLAB
- MATLABでアフィン行列の合成を確認。
- 問題無く動作。
- 回転行列内の三角関数に渡す角度は度数法ではなく弧度法。
- 180で割ってπを掛ける。
- 変換しない際は単位行列になるようにしておけば、掛けても影響はない。
Python
- Python(NumPy)でアフィン行列の合成を実施。
- 問題無く動作。
- 三角関数ははNumPyが持っているものを使用。
- 他のライブラリも三角関数を持っていることが多い。
- 精度の違い等があるかもしれないが調べてない。
- 他のライブラリも三角関数を持っていることが多い。
Scilab
- Scilabでアフィン行列の合成を実施。
- 問題無く動作した。
- Scilabの変数名、関数名の文字数は最大で24文字。
Julia
- Juliaでアフィン行列の合成を実施。
- 問題無く動作した。
- 毎度のことながらmeshgridは自作関数。
- 毎度のことながら2回目以降の実行処理速度は最速。
- 同じようなことを繰り返しで実行、試行錯誤する場合は便利。
射影変換
- 射影変換はアフィン変換の拡張と言われいるが、理屈としては異なるもの。
- 射影変換で出来ることを確認。
- 射影変換は四隅の点をどこに移動させるかという変換。
- 長方形から台形、台形から長方形、台形から台形。
- 射影変換の理屈を把握するための流れを記載。
- 変換過程を説明。
- 変換過程毎の数式化、方程式化、行列化を実施。
- 射影変換とアフィン変換との関係性について説明。
- 上記を元に8個の変数を求める8個の連立方程式を作成し行列表現に。
- 射影逆変換について説明。
MATLAB
- MATLABで射影変換を実施。
- 処理はアフィン変換の時のモノを流用。
- 射影変換のsの部分を追加で解決しているのみ。
Python
- Python(NumPy)で射影変換を実施。
- アフィン変換が出来ていれば、射影変換の処理を作るのはそれほど難しくない。
Sclilab
- Scilabで射影変換実施。
- 基本的にはMATLABと一緒で、射影変換のsを解決するコードを追加すればOK。
Juia
- Juliaで射影変換実施。
- 基本的にはMATLABと一緒で、射影変換のsを解決するコードを追加すればOK。
射影変換(台形→長方形)
- 射影変換で台形から長方形への変換もできるはず。
- 台形から長方形にする際に引き延ばした部分の画像は荒くなる。
- プログラム化自体は以前のものを使い回し。
MATLAB
- MATLABで射影変換の台形から長方形の変換を実施。
- 想定通り変換。
- 画像は荒くなるが想定通り。
- 変換元、変換先パラメータを調整するだけで実現可能。
Python
- Python(NumPy)で射影変換の台形から長方形の変換を実施。
- 想定通り変換。
- コードの流れと構成はMATLAB時のコードと一緒なため、パラメータ調整箇所も一緒。
Scilab
- Scilabで射影変換の台形から長方形の変換を実施。
- 想定通り変換。
- コードの流れと構成及び文法的にもMATLAB時のコードと一緒なため、パラメータ調整箇所も一緒。
Julia
- Juiaで射影変換の台形から長方形の変換を実施。
- 想定通り変換。
- コードの流れと構成及び文法的にもMATLAB時のコードと一緒なため、パラメータ調整箇所も一緒。
- 今回は座標変換なため影響はないが色情報の持ち方が256階調ではなく、0~1に正規化されてる点に注意。
射影変換、アフィン変換合成
- 射影変換は数式上はアフィン変換の拡張型。
- 射影変換のアフィン行列を入れてアフィン変換になるか試そうと画策。
- 射影変換、アフィン変換合成時のパラメータを(テキトーに)決めた。
MATLAB
- 射影変換とアフィン変換の合成をMATLABで実施。
- 問題無く動作。
- 複数の座標変換だが、事前にパラメータを合成することで処理としては一回にまとめられる。
Python
- 射影変換とアフィン変換の合成をPython(NumPy)で実施。
- 問題無く動作。
- 射影変換にアフィン変換行列を渡せば、アフィン変換ができることを知っていればOK。
Scilab
- 射影変換とアフィン変換の合成をScilabで実施。
- メモリ不足問題に直面しやすいが一応動作した。
- 行列定義の仕方はMATLABと一緒なので、コピペした。
Julia
- 射影変換とアフィン変換の合成をJuliaで実施。
- 問題無く動作した。
- 行列の定義の記述はMATLABと一緒なのでコピペ。
- すごく似ているが故にハマることもある。
次のページへ
次のページでは分類問題。
形式ニューロン、単純パーセプトロン、多層パーセプトロン(ニューラルネットワーク)など。







































































コメント