Pythonで動かして学ぶ!あたらしい線形代数の教科書
波形表示方法
基本的にはすべて同一。
同一のグラフに描画する際の方式が若干異なる。
MATLAB:事前にhold on。
Python:最後にshow()
Scilab:デフォルトで同一グラフに描画。
とりあえず、以下な感じのグラフを出す。
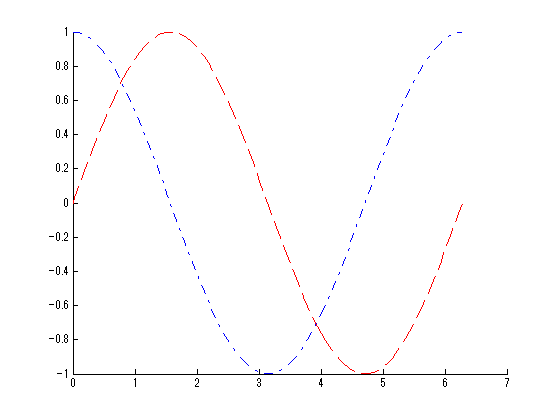
MATLABの波形表示方法
Pythonの波形表示方法
Scilabの波形表示方法
Juliaの波形表示方法
伝達関数使用方法
ゼロからはじめるPID制御
MATLABは「control system toolbox」(別途費用発生)が必要。
これを理由にPython,Scilabに一時的に逃げたという背景もある。
PythonのcontrolパッケージはMALABの「control system toolbox」の仕様を踏襲しているらしい。まじめに比較すると演算速度とかで差があるのかもしれないが、まずはお試しレベルであれば、いろいろと実験が捗る。
Scilabは、特にMATLABを踏襲することは無く、独自のシミュレーション関数で実現している。
使い熟すにはやや難易度が高が、一つのパターンを覚えてしまえば、使い回しが利く。
Pythonの伝達関数使用方法
Scilabの伝達関数使用方法
状態空間モデル超基礎
Pythonによる制御工学入門
- 状態空間モデルに苦手意識持ってる人向けに超シンプルな微分方程式に対して適用して見た。
- ニュートンの運動方程式を採用。
- 状態量が求まる微分方程式を作成すると、それを状態方程式として表現できる。
- 参照したい状態量を出力行列で設定できる。
状態空間モデル(運動方程式)
MATLAB/Simulink状態空間モデル(運動方程式)
- MATLAB/Simulinkで状態空間モデルのシミュレーション。
- 必要ブロックはState-Space、Step、Scope、Mux。
- 状態空間モデルの各行列の設定はState-Spaceの詳細設定で可能。
- シミュレーションは摩擦等を無視しているので宇宙空間での挙動
Python状態空間モデル(運動方程式)
- Pythonで状態空間モデルを扱うには、controlライブラリのmatlabモジュールが必要。
- 仕様的にはMATLABのControl System Toolboxを踏襲している。
- ss関数に各行列を渡し、システムオブジェクトを取得。
- lsimに入力のstep信号をシステムオブジェクトを渡してシミュレーション。
Scilab状態空間モデル(運動方程式)
- Scilabで状態空間モデルのシミュレーションをするにはsyslinとcsim関数を使用する。
- MATLABに寄せてるかと思いきや、この分野はかなり異なる仕様になっている。
- 今回の状態空間モデルに限定するとたまたま流れが似ていただけ。
- MATLABに寄せてるかと思いきや、この分野はかなり異なる仕様になっている。
Julia状態空間モデル(運動方程式)
- Juliaで状態空間モデルをシミュレーション。
- Pythonと同じくMATLAB Control System Toolboxの仕様を踏襲したControlSystemsパッケージを使用。
- 結局はMATLAB Control System Toolboxの仕様がデファクトスタンダード感がある。
- Pythonと同じくMATLAB Control System Toolboxの仕様を踏襲したControlSystemsパッケージを使用。
微分方程式からCコードを作成
- 状態空間モデルを使用せず、微分方程式のままシミュレーションを試みる。
- Simulinkがあれば、ブロック図のままでもシミュレーションできるが…。
- その後、ブロック図を離散化。
- この段階でオートコード生成したりもする。
- 漸化式導出。
- Cコード化とシミュレーション実施。
- もっとも原始的なモデルベース開発?
状態空間モデルで微分解決
- 状態空間モデルの状態方程式と出力方程式の微分解決を実施。
- 基本的には状態方程式側の微分解決をし、その結果を出力方程式に代入する。
- MATLAB、Python、Scilab、Juliaで上記をプログラムとして実装予定なので、よくわからん人は参照すべし。
状態空間モデルで微分解決(MATLAB)
- MATLABでベクトル、行列演算による状態空間モデルの演算実施。
- 導出した数式のまんまでコードが組める。
- このルールに即していれば、さまざまな振る舞いを規定できる。
- シミュレーション結果も想定通り。
状態空間モデルで微分解決(Python)
- Python(Numpy)でベクトル、行列演算による状態空間モデルの演算実施。
- 流れとしてはMATLABと同一。
- 内積の演算子が「@」な点に注意。
- シミュレーション結果も想定通り。
状態空間モデルで微分解決(Scilab)
- Scilabでベクトル、行列演算による状態空間モデルの演算実施。
- MATLABと同一。
- グラフ表示の部分に差異があるだけ。
- シミュレーション結果も想定通り。
状態空間モデルで微分解決(Julia)
- Juliaでベクトル、行列演算による状態空間モデルの演算実施。
- MATLABとほぼ同一。
- 添え字、ドット演算子に違いあり。
- シミュレーション結果も想定通り。
状態空間モデルで微分解決(C言語)
- Cコードによるベクトル、行列演算による状態空間モデルの演算実施。
- MATLAB Coderで出力。
- シミュレーション結果も想定通り。
- コード自体は複雑になるが、多変量の微分方程式になった際に効果は大きくなる。
状態空間モデル(DCモータ)
- DCモータ状態空間モデルを導出するため以下を実施。
- 状態量の定義。
- 各種微分方程式。
- 微分方程式の変形。
- 状態方程式の作成。
- 出力方程式の作成。
- 確からしさはシミュレーションで確認。
状態空間モデル(DCモータ)MATLAB
- DCモータ状態空間モデルをMATLABでシミュレーション。
- 状態空間モデルを演算する関数自体はそのまま使い回し。
- シミュレーションとしては想定通りの結果。
状態空間モデル(DCモータ)Python
- DCモータ状態空間モデルをPython(Numpy)でシミュレーション。
- 流れとしてはMATLABと一緒。
- 状態空間モデルの演算用関数が変化しない特徴も一緒。
- シミュレーションも同一であり、想定通り。
状態空間モデル(DCモータ)Scilab
- DCモータ状態空間モデルをScilabでシミュレーション。
- 演算自体はMATLABと同一。
- 差はグラフ表示の微調整のところ。
- シミュレーションも同一であり、想定通り。
状態空間モデル(DCモータ)Julia
- DCモータ状態空間モデルをJuliaでシミュレーション。
- かなりMATLABと近似のコードになる。
- linspaceがrangeになってるくらい。
- シミュレーションも同一であり、想定通り。
状態空間モデルをPID制御
- DCモータの状態空間モデルを制御するためPID制御器を追加する。
- 上記を実現するためPID制御器の離散化を行う必要がある。
- PID制御器は速度型PIDとする。
- ワインドアップ対策の都合、速度型PIDを使うことが多い。
- 数式は複雑っぽく見えるがブロック線図としてはシンプル。
状態空間モデルをPID制御(MATLAB)
- PID制御器のブロック線図と全体構成を再掲。
- 上記をMATLABで実現。
- 接続に関してはコード上では分かり難いので全体構成図と見比べながら確認した方が良い。
- シミュレーション実施。
- u(t)の挙動と見るとPID制御っぽい挙動になっている。
- 各PIDゲインを調整すると挙動が変わるはず。
- u(t)の挙動と見るとPID制御っぽい挙動になっている。
状態空間モデルをPID制御(Python)
- MATLABでやったDCモータ状態空間モデルをPID制御をPython(Numpy)で実施。
- Pythonの場合、構造体はclassで実現。
- 事前にclassを定義する必要はある。
- MATLABと同様の結果が得られた。
状態空間モデルをPID制御(Scilab)
- ScilabでDCモータ状態空間モデルをPID制御シミュレーション実施。
- コード自体はMATLABと一緒。
- 構造体の生成の仕方も一緒だが、内部的には連想配列で実現されている。
- シミュレーション結果もOK。
状態空間モデルをPID制御(Julia)
- JuliaでDCモータ状態空間モデルをPID制御シミュレーション。
- Juliaも構造体を定義できるが、structだと更新不可になる。よってmutableを使って更新可能な構造体にする必要がある。
- シミュレーション結果は他のツール言語と同じ結果が得られた。
次のページへ
次ページから最小二乗法等の回帰分析について































コメント