バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
前回までで複素フーリエの話がおおよそ終わったところだが、
実数フーリエの時と同様に周期が2π限定になっているため、
周期を任意にできるようにする必要がある。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
任意周期

とりあえず複素フーリエも完了かな。

いんや。まだだ。

え゛

現状の複素フーリエは、周期が\(2\pi\)が前提になってしまっている。

そういえば、実数フーリエの時も同じ話があったな・・・。

というわけで、複素フーリエも任意周期に対応させる。
周期2L

複素フーリエの任意周期化も実数フーリエと同じアプローチになる。

確か、\(2\pi\)を\(2L\)に置き換えるって感じだったね。

画像で示すと以下になる。
まぁ、実数フーリエの時と同じものだな。
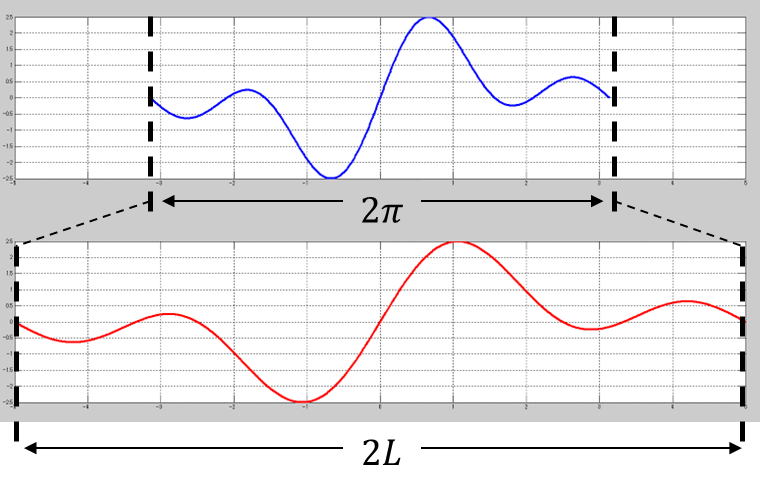

ちなみに、0を中心とした\(2\pi\)の範囲の線対称は、cos関数の影響だな。
sin関数は奇関数なので0中心であれば、積分時に必ず0になるが、
cos関数の方は偶関数のため、\(2\pi\)の範囲でないと積分時に0にならない、
これは直交性に影響する話になる。

そこは実数フーリエの時にも言ってたね。
複素フーリエでは複素指数関数ではあるけど、
オイラーの公式から、結局はcos関数とsin関数の組み合わせであることは変わらないから、同じ理屈になるってことだね。

そうそう。

次回から実際に任意周期化をしてみよう。
まとめ

まとめだよ。
- 前回までの複素フーリエは、周期が2πという制約がある。
- 2πを2Lに変換することで任意周期に対応させる。
- このアプローチは実数フーリエの時と同じ。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす


コメント