バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
任意波形から複素フーリエ係数抽出。
それを元に元波形を複素フーリエ級数で再現。
これをJuliaで実施する。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】プログラムフロー

太郎くん
まずはプログラムフローの再掲。
- csvファイル読み込み
- 各種変数初期化
- フーリエ係数算出
- n=10,50,200のパターンでフーリエ級数で波形を合成
- グラフにプロット

フクさん
これをJuliaで実現する。
Juliaコード

フクさん
使用するcsvファイルはこれ。

フクさん
Juliaコードは以下。
using PyPlot
using CSV
using DataFrames
using Printf
N=1000; # 係数算出項数(同定元波形のplotよりも少なく)
csv_data=CSV.read("wave.csv", DataFrame); # 同定波形読み込み
wave = csv_data[:,1];
points=length(wave); # 波形のplot数取得
fx=wave'; # 波形を行ベクトルへ
dx=2*pi/points; # 1plotあたりのx軸幅
x=range(-pi,pi,length=points); # -π~+πの範囲で波形plot数分の等差数列
C = zeros(Complex{Float64},1,N*2+1); # C係数群格納用(±両方)
for n = -N:N
# 係数C_n算出
# C[N+1]がC_0
# C_n = (1/2π)∫f(x)exp(-inx)dx
C[n+N+1] = fx*exp.(-1im*n*x)*dx/(2*pi);
end
Ns = [10,50,200];
for i = 1:length(Ns)
NN = Ns[i]; # 今回のC_n項数
# f(x)=Σ(C_n exp(inx))
Fourier_series = zeros(1,points); # 合成関数を0初期化
for n = -NN:NN
Fourier_series = Fourier_series+(C[n+N+1]*transpose(exp.(1im*n*x)));
end
# 元波形と複素フーリエ級数波形の表示
subplot(length(Ns),1,i);
plot(x, fx,linewidth = 3);
plot(x, real(Fourier_series)',color="r", linewidth = 2);
title(@sprintf("n=±%d",NN), fontsize=22, fontweight="bold");
ylim([-0.1,1.1]);
xlim([-pi,pi]);
grid();
end処理結果

フクさん
処理結果は以下。
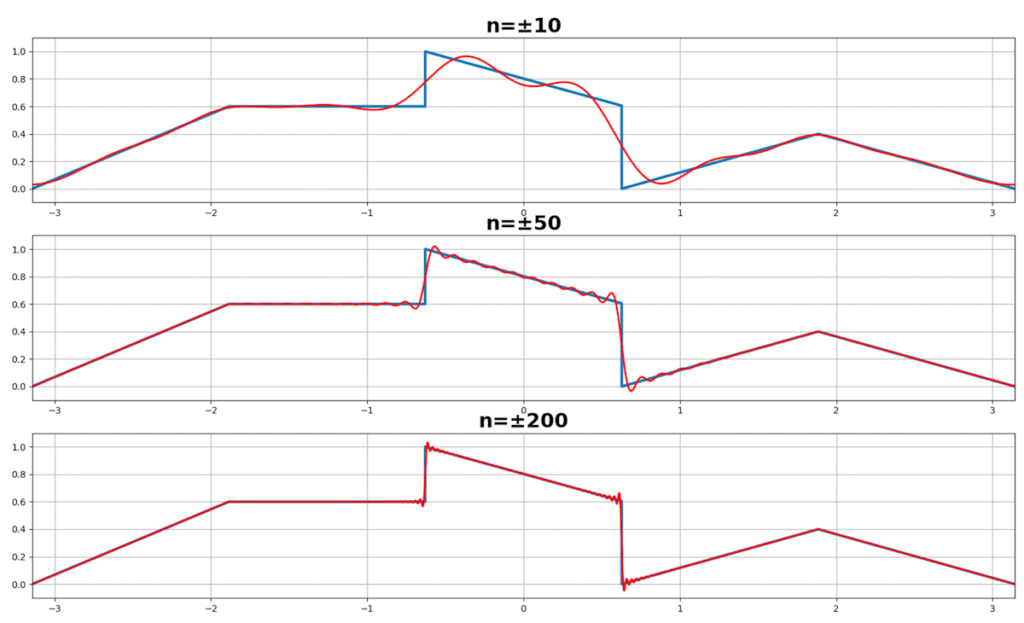

太郎くん
これも実数フーリエのときと同じ結果だね。

フクさん
位相とかを調べたい場合は、複素平面上の偏角を求めたりする。
まとめ

フクさん
まとめだよ。
- 任意波形から複素フーリエ係数抽出し、それを元に元波形を複素フーリエ級数で再現をJuliaで実施。
- 実数フーリエと同じ結果が得られた。
- 係数は複素数であり、偏角から位相を求めることも可能。
バックナンバーはこちら。
マンガでわかるフーリエ解析
Amazon.co.jp
手を動かしてまなぶ フーリエ解析・ラプラス変換
手を動かしてまなぶ フーリエ解析・ラプラス変換 | 山根 英司 | 数学 | Kindleストア | Amazon
Amazonで山根 英司の手を動かしてまなぶ フーリエ解析・ラプラス変換。アマゾンならポイント還元本が多数。一度購入いただいた電子書籍は、KindleおよびFire端末、スマートフォンやタブレットなど、様々な端末でもお楽しみいただけます。
物理数学 量子力学のためのフーリエ解析・特殊関数
Amazon.co.jp
単位が取れるフーリエ解析ノート
Amazon.co.jp
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす
Amazon.co.jp




コメント