バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
マクローリン展開のおおよその説明をしたところ。
今回は、sin関数のマクローリン展開をPythonで演算しプロットするプログラムを作成
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】sin関数のマクローリン展開

まずは、sin関数のマクローリン展開を再掲。
\(
\begin{eqnarray}
\displaystyle f(x)&=&f(0)+\frac{f^\prime(0)}{1!}x+\frac{f^\prime\prime(0)}{2!}x^2+\dots\\
\displaystyle &=&f(0)+\sum_{n=1}^\infty\frac{f^n(0)}{n!}x^n\\
\displaystyle \sin(x)&=&x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots\\
\displaystyle &=& \sum_{n=0}^\infty\frac{(-1)^n x^{2n+1}}{(2n+1)!}
\end{eqnarray}
\)

今回はPythonでsin関数のマクローリン展開をMATLABで演算&プロットする。
【再掲】sin関数のマクローリン展開のプログラムフロー

そして、プログラムフローも再掲。
- プロット数、プロット範囲、x軸の定義
- nの次数列を定義
- 次数列に応じて以下を繰り返す
- sin関数のマクローリン級数を演算
- 演算結果をプロット
Pythonコード

Pythonコードは以下。
import numpy as np
import matplotlib.pyplot as plt
P=1000 # プロット数
L=2*np.pi # -L~+Lの範囲
x=np.linspace(-L,L,P) # x軸
Ns = [0,1,2,3,4,5] # n数セット
K=len(Ns)
fig = plt.figure()
for i in range(1,K+1):
N=Ns[i-1] # n数
Maclaurin_series = np.zeros(P)
# Σ(-1)^n x^(2n+1) / (2n+1)!
for n in range(0,N+1):
Maclaurin_series = Maclaurin_series + ((-1)**n)*(x**(2*n+1))/np.math.factorial(2*n+1)
ax = fig.add_subplot(3,int(np.ceil(K/3)),i)
ax.plot(x, np.sin(x),'-b',lw=3)
ax.plot(x, Maclaurin_series,'-r',lw=2)
ax.set_title('n={:d}'.format(N),fontsize=22,fontweight="bold")
ax.set_xlim([-L,L]);
ax.set_ylim([-1.5,+1.5])
ax.grid(linestyle='dotted')
plt.show()処理結果

処理結果は以下。
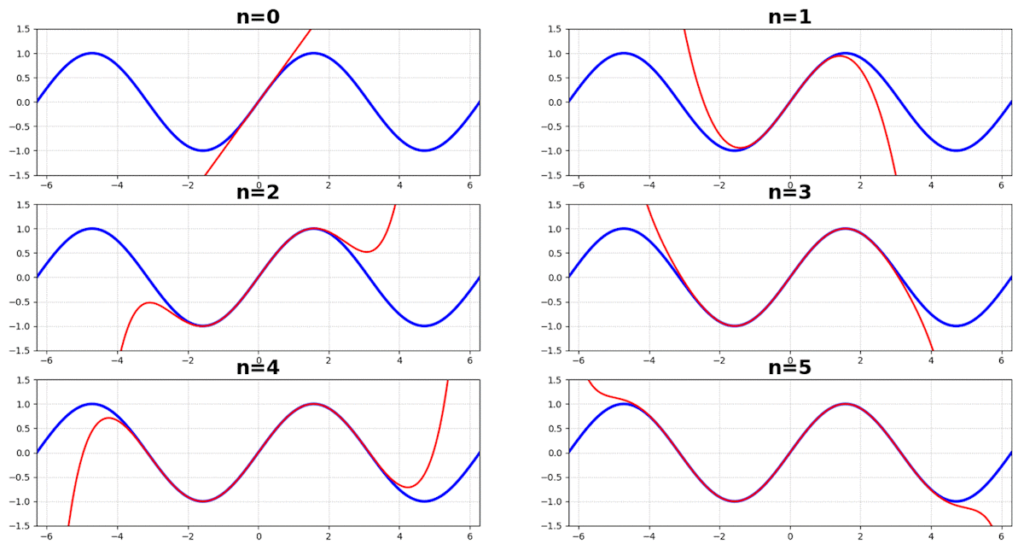

nが増えていけばsin関数になるのが分かるね。
まとめ

まとめだよ。
- sin関数のマクローリン展開の演算とプロットをPythonで実施。
- nが増えればsin関数に近似していく。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント