バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
前回で、フーリエ級数、フーリエ係数を周期2πという制約を外して、
周期2Lという任意の周期で対応できるように改造した。
今回は、これをプログラムに落とし込むための話。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
プログラム化可能か?

ここらへんで一度プログラムで確認しておきたいところだね。

そうだね。
基本的には以前のフーリエ級数、フーリエ係数の流れと変わらない。
扱う数式が変わるだけだ。

元の波形とかはどうするの?

以前のものを使い回しだな。
csv形式のファイルに波形情報を入れているが、
特に時間の指定はしていない。
前回は\(-\pi\sim\pi\)として取り込んだところを。
\(-L\sim L\)と解釈し直せばOKだ。

つまりおおよそ使い回しが効きそうってことか。
想定される結果

一応、想定される結果を出しておこう。
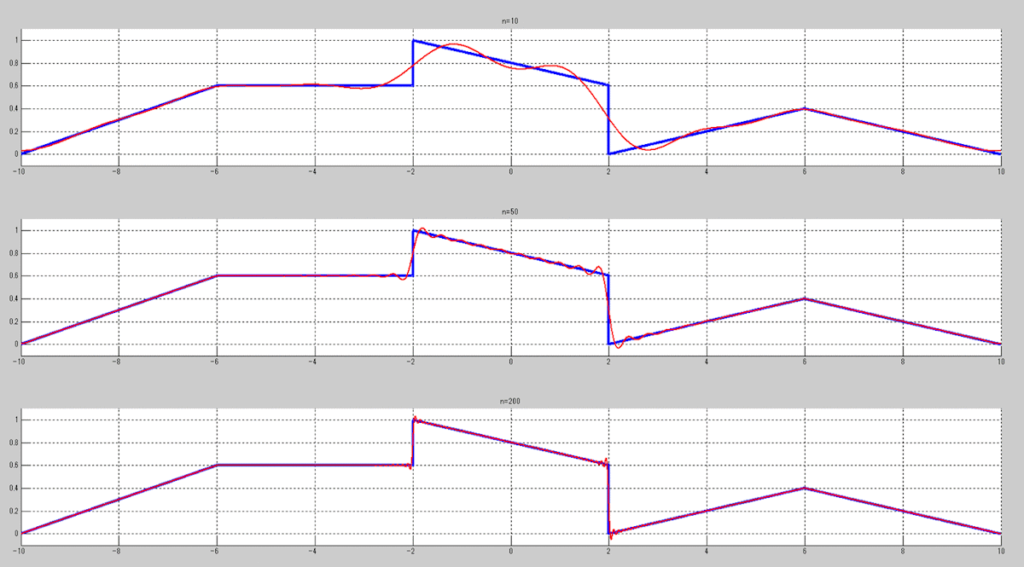

元のcsvデータが一緒だから、波形の形状は同一だけど、
横軸の値が\(-10\sim 10\)に代わってるね。

そうそう。
これが任意周期にすることで得られる効能だな。
プログラムフロー

プログラムフローも記載するが、基本的には前回と一緒だ。
- csvファイル読み込み
- 各種変数初期化
- フーリエ係数算出
- n=10,50,200のパターンでフーリエ級数で波形を合成
- グラフにプロット

全く一緒だ。

csvファイルの想定周期、
使用するフーリエ級数、フーリエ係数の数式を差し替えて、
期待される結果が得られるかというのが確認ポイントとなるな。

周期が任意設定できるとなると、割と使いやすい感じになりそうだね。
まとめ

まとめだよ。
- 任意周期のフーリエ級数、フーリエ係数のプログラム化検討。
- 基本的には以前の使い回し。
- 波形データの解釈や、数式が変わるのみ。の予定。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント