バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
前回まででフーリエ係数を求めることを試した。
が、現状のフーリエ級数、フーリエ係数にはとある制約が掛かっている・・・。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
現状のフーリエ級数、フーリエ係数にはとある制約

とりあえず、フーリエ級数とフーリエ係数はバッチリってことだね。

まだだ。

え゛

前回までやったフーリエ級数、フーリエ係数にはとある制約が掛かっている。

制約?

波形の周期が\(-\pi\sim\pi\)の\(2\pi\)の範囲と言う制約だな。
この制約は、三角関数の直交性を得る上での制約なる。
特に偶関数であるcos関数などは、\(2\pi\)の周期じゃないと、積分した結果が0とならず、
直交性が得られない場合が発生してしまう。

フーリエ係数の式を見てもその制約が垣間見える。
\(
\begin{eqnarray}
\displaystyle a_n&=&\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(nx)dx\\
\displaystyle b_n&=&\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(nx)dx\\
\displaystyle a_0&=&\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx
\end{eqnarray}
\)

なるほど・・・。
この制約はなんとなく使い勝手がわるそうなイメージがある・・・。
結局どうしたら良いのか?

制約があるのはわかったけど、
これって何か対策とかあるの?

フーリエ級数の中の角周波数を調整して、周期を任意の幅にするというのが一般的だな。

何言ってるのかわからん・・・。

図にするとこのイメージだな。
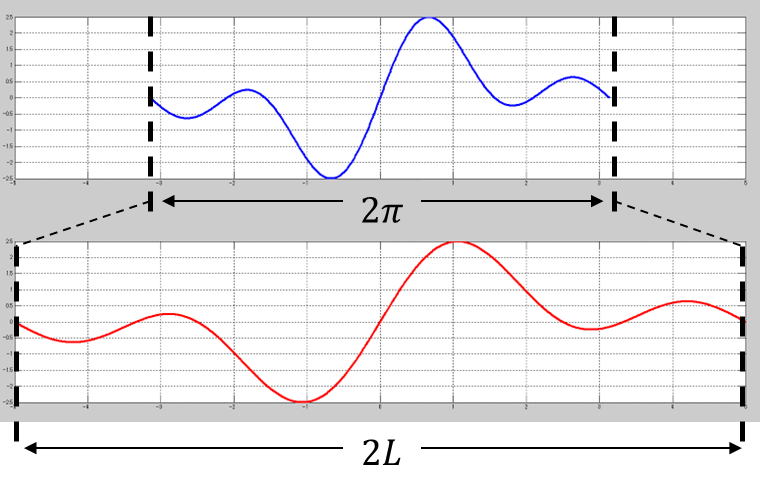

単純に伸縮するって感じかな?

その認識で問題無い。

問題はどうすれば伸縮できるのかってところだな・・・。

そこは次回解説しよう。
まとめ

まとめだよ。
- 前回までのフーリエ級数、フーリエ係数には周期2πという制約がある。
- 三角関数の直交性を得るための制約。
- 周期を変えるには、周期の伸縮を考えると解決できるかも?
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント