バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
フーリエ係数に至る道。
今回は重要な極限値について説明。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】フーリエ係数に至る道

まずは、フーリエ係数に至る道を再掲。
- 偶関数
- 奇関数
- 関数の内積
- 三角関数の加法定理
- 三角関数の積和公式
- 重要な極限値
- 三角関数の直交性
- フーリエ係数

今回は重要な極限値の説明になる。
重要な極限値とは?

で、重要な極限値って何?

以下の極限値だな。
\(
\displaystyle\lim_{x\to0}\frac{\sin(x)}{x}
\)

\(x\)を限りなく\(0\)に近づけた場合の\(\sin(x)/x\)ってことなんだろうけど、
\(sin(0)=0\)だから、\(0/0\)になって不定値になるパターンに見えるな・・・。

単純に0を代入するとそうなるね。
そこで極限値であることが重要になってくる。

つまり、いきなり0を代入するのではないく、徐々に0に近づけていくと、
何かしらの値に収束するってことか。

そうそう。
円に接する三角形と扇形に着目する

これを解くには縁に接する三角形と扇形に着目する必要がある。

何を言ってるのかわからん・・・。

絵に描くとこんなやつだ。
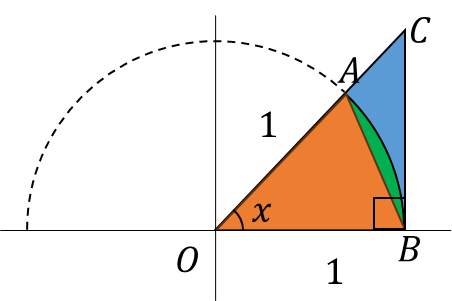

絵にされても意味がわからん・・・。

まぁ、この絵と先ほどの関数の直接的な関係性はないからね。
各図形の面積に着目すると以下の不等式が成立する。
\(
{\color{orange}三角形OAB}<{\color{green}扇形OAB}<{\color{blue}三角形OBC}
\)

まぁ、確かに成立するのは先ほどの絵を見るとあってそう。

さらに、それぞての面積を求める。
半径1の円に接しているので、底辺が1になっているのがポイントだな。
\(
\begin{eqnarray}
\displaystyle{\color{orange}三角形OAB}&=&底辺\times高さ\div2=\frac{1}{2}\sin(x)\\
\displaystyle{\color{green}扇形OAB}&=&\pi r^2\frac{x}{2\pi}=\frac{1}{2}x\\
\displaystyle{\color{blue}三角形OBC}&=&底辺\times高さ\div2=\frac{1}{2}\tan(x)
\end{eqnarray}
\)

一見すると面積とか求められない気がしたけど、
冷静にみれば、面積を求めるための情報は揃っていたってことか。

そうそう。
あとは、これらを利用して数式を変形していく。
まとめ

まとめだよ。
- 重要な極限値について説明。
- sin(x)/xのxを0に近づける極限値。
- まずは円に接する三角形と扇形に着目する。
- これが先ほどの極限値にどうつながるかは次回。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント