バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
フーリエ係数に至る道。
今回は偶関数と奇関数を利用した数学パズルを割と真面目に解くバージョン。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】フーリエ係数に至る道

まずは、フーリエ係数に至る道を再掲。
- 偶関数
- 奇関数
- 関数の内積
- 三角関数の加法定理
- 三角関数の積和公式
- 重要な極限値
- 三角関数の直交性
- フーリエ係数

今回は偶関数と奇関数を利用した数学パズルを割と真面目に解くバージョン。
前回の数学パズルを真面目に解く?

前回は、なぞの定積分を偶関数と奇関数の特性を利用すると解けてしまうって話だったね。

前回は、比較的大雑把に解いた感じだ。
今回は、これを真面目に解いてみる。

(真面目かぁ・・・)
数式を展開

まずは元の数式を展開する。
\(
\begin{eqnarray}
&&\displaystyle\int_{-2}^2\Big(x^3\cos(2x)+\frac{1}{2}\Big)\sqrt{4-x^2}dx\\
&=&\displaystyle\int_{-2}^2\Big(x^3\cos(2x)\sqrt{4-x^2}+\frac{1}{2}\sqrt{4-x^2}\Big)dx
\end{eqnarray}
\)

まぁ、ここは普通だな。
平方根の関数の正体を探る

ここで問題になるのか、
\(\sqrt{4-x^2}\)が何者かという点。

前回の話だと半円の方程式とか言ってたね。

そうそう。
三平方の定理から求められるのだけど、
少し図を交えて説明する必要がある。
まず三平方の定理を確認しよう。
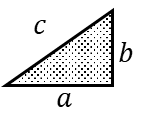

これを三平方の定理で表現すると以下になる。
\(
c^2=a^2+b^2
\)

ここはわかる。

これを原点と円周の任意の点と、その点から垂直方向に落とした点を\(x\)で構成された三角形として考える。
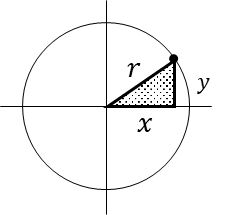

三平方の定理を使うと以下が成立する。
\(
r^2=x^2+y^2
\)

yとして解くと、
\(
y=\sqrt{r^2-x^2}
\)

つまり、\(\sqrt{4-x^2}\)は\(r=2\)の半円の方程式ということになる。
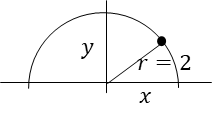

なるほど。
こういう理屈で半円の方程式と特定できるのか。

半円なので、偶関数と言うことになる。
これでそれぞれの関数が偶関数、奇関数と判明したことになるな。

あとは、偶関数、奇関数の特性を利用して解けば良いのか。
まとめ

まとめだよ。
- 前回の数学パズルを真面目に解いてみる。
- まずは平方根の関数の正体を探る。
- 結果としては半円の方程式と言うことになる。
- これで構成される関数が偶関数か奇関数か特定できたことになる。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント