バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
ニューラルネットワークの最適化アルゴリズムについて。
前回はモーメンタムの更新式の話、今回はモーメンタムの動作イメージについて。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
モーメンタムへ至る道【再掲】

まずはモーメンタムへ至るフローを再掲
- 勾配降下法の更新式(済)
- 勾配降下法の動作イメージ(済)
- モーメンタムの更新式(済)
- モーメンタムの動作イメージ
- モーメンタムのプログラムフロー
- モーメンタムによる分類の学習プログラム

今回は、この中の「モーメンタムの動作イメージ」
モーメンタムの動作イメージ

で、モーメンタムの動作イメージはどうなるの?

モーメンタムの動作イメージはなかなか表現しずらいのだが、
こんな表現になるな。
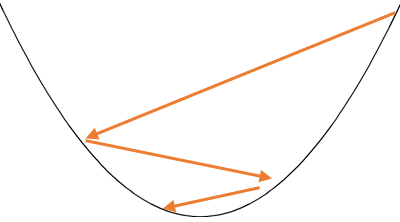

イマイチわからん・・・。

基本的には最初は大きく動いて、収束するにつれて更新値が小さくなる。
これは過去の勾配がどれだけ大きいかに依存した動きになるな。

つまり、
最初は恐らく勾配が大きいから、大き目に動く。
その内、最適解に近付いてくるから、その段階で更新値が小さくなって、
細かい最適解を見つけてくれるって感じか。

そうだね。
学習率自体は固定なのだが、
更新値は状況に応じて可変。
これは勾配降下法の観点で見ると学習率が状況に応じて可変と同義になるな。

学習率が固定だと、適正な値を探す必要があったけど、
モーメンタムだとある程度自動で変化するってことか。

そうそう。
少なくとも最初は大きく動くから最適解までの収束ステップは少なくなるはずだ。

シンプルな更新式ではあるけど、
効果は大きそうだね。

そうだね。
とりあえず、まず試しても良いレベルのお手軽さだろう。
まとめ

まとめだよ。
- モーメンタムの動作イメージについて確認。
- 動作イメージの表現は難しい。
- 最初は大きく更新して、最適解が近いと小さく更新。
- 勾配降下法で言うところの学習率が可変と同義な動きになる。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント