MATLAB,Python,Scilab,Julia比較 第4章 その81【誤差逆伝播法⑧】

バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/

はじめに
登場人物
誤差逆伝播法の各演算【再掲】
Pythonコード
処理結果
まとめ

はじめに

多層パーセプトロンの誤差逆伝播法を行う。
今回はPythonで実現。

登場人物

博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1

エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1

誤差逆伝播法の各演算【再掲】

太郎くん

まずは、前回求めた誤差逆伝播法の各演算を再掲。

隠れ層の重み\(W_2\)とバイアス\(b_2\)の勾配(\(\Delta W_2,\Delta b_2\))を特定

\(
\Delta W_2=\Delta_2 A_2
\)

\(
\Delta b_2=\Delta_2 1
\)

入力層の重み\(W_1\)とバイアス\(b_1\)の勾配(\(\Delta W_1,\Delta b_1\))を特定

\(
\Delta W_1=\Delta_1 X
\)

\(
\Delta b_1=\Delta_1 1
\)

各勾配から各重み、各バイアスを更新(学習率\(\mu\)を掛けておく)

\(
\begin{eqnarray}
W_1&=&W_1-\mu\Delta W_1\\
b_1&=&b_1-\mu\Delta b_1\\
W_2&=&W_2-\mu\Delta W_2\\
b_2&=&b_2-\mu\Delta b_2\\
\end{eqnarray}
\)

フクさん

これをPythonで実現する。

Pythonコード

フクさん

Pythonコードは以下。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

# データの準備
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])  # 入力データ
y = np.array([[0], [1], [1], [0]])  # 出力データ

# ネットワークの構築
hidden_size = 2  # 隠れ層のユニット数
output_size = 1  # 出力層のユニット数
learning_rate = 0.5  # 学習率

input_size = X.shape[1]
W1 = np.random.randn(input_size, hidden_size)  # 入力層から隠れ層への重み行列
b1 = np.random.randn(1, hidden_size)  # 隠れ層のバイアス項
W2 = np.random.randn(hidden_size, output_size)  # 隠れ層から出力層への重み行列
b2 = np.random.randn(1, output_size)  # 出力層のバイアス項

# 学習
epochs = 4000  # エポック数

errors = np.zeros((epochs, 1))  # エポックごとの誤差を保存する配列

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    return sigmoid(x) * (1 - sigmoid(x))

for epoch in range(epochs):
    # 順伝播
    Z1 = X@W1 + b1 # 隠れ層の入力
    A1 = sigmoid(Z1)  # 隠れ層の出力
    Z2 = A1@W2 + b2 # 出力層の入力
    A2 = sigmoid(Z2)  # 出力層の出力

    # 誤差計算（平均二乗誤差）
    error = (1 / X.shape[0]) * np.sum((A2 - y) ** 2)
    errors[epoch] = error

    # 逆伝播
    delta2 = (A2 - y) * sigmoid_derivative(Z2)
    delta1 = np.dot(delta2, W2.T) * sigmoid_derivative(Z1)

    grad_W2 = A1.T@delta2
    grad_b2 = np.sum(delta2, axis=0)
    grad_W1 = X.T@delta1
    grad_b1 = np.sum(delta1, axis=0)

    # パラメータの更新
    W1 = W1 - learning_rate * grad_W1
    b1 = b1 - learning_rate * grad_b1
    W2 = W2 - learning_rate * grad_W2
    b2 = b2 - learning_rate * grad_b2

# 決定境界線の表示
h = 0.01  # メッシュの間隔
x1, x2 = np.meshgrid(np.arange(np.min(X[:, 0]) - 0.5, np.max(X[:, 0]) + 0.5, h),
                     np.arange(np.min(X[:, 1]) - 0.5, np.max(X[:, 1]) + 0.5, h))
X_mesh = np.c_[x1.ravel(), x2.ravel()]

hidden_layer_mesh = sigmoid(np.dot(X_mesh, W1) + b1)
output_layer_mesh = sigmoid(np.dot(hidden_layer_mesh, W2) + b2)
y_mesh = np.round(output_layer_mesh)  # 出力を0または1に丸める

decision_mesh = y_mesh.reshape(x1.shape)  # 分類結果のメッシュを元のグリッドサイズに変形する
colormap = ['#CCFFCC','#FFCCCC']  # 各領域の色を指定する
plt.contourf(x1, x2, decision_mesh, levels=1, colors=colormap)  # カラーマップを適用する
plt.scatter(X[y.flatten() == 1, 0], X[y.flatten() == 1, 1], color='r', marker='o', label='Class 1')  # クラス1のデータ点を赤でプロット
plt.scatter(X[y.flatten() == 0, 0], X[y.flatten() == 0, 1], color='g', marker='o', label='Class 0')  # クラス0のデータ点を緑でプロット
plt.xlabel('X1')
plt.ylabel('X2')
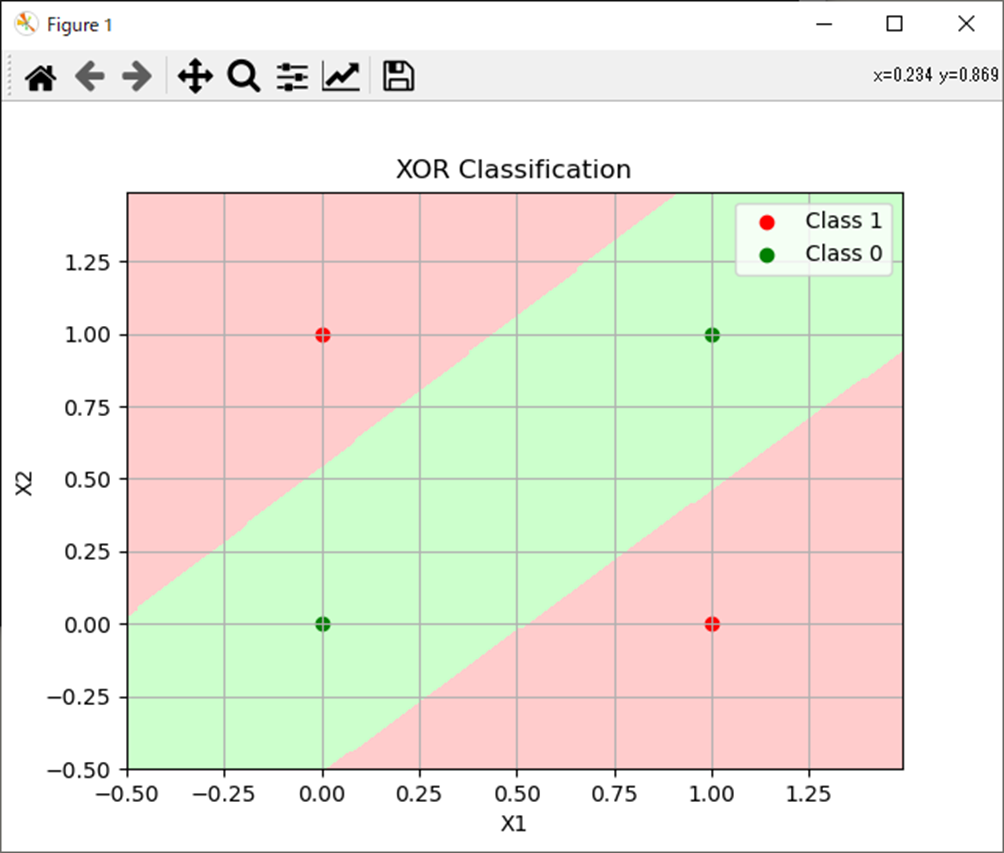
plt.title('XOR Classification')
plt.legend(loc='best')
plt.grid()
plt.show()