バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
単純パーセプトロンで分類を行う。
逆伝播の復習を行いつつ、分類の方法を考える。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
単純パーセプトロンの構造

前回までで、逆伝播の話が終わった。

重みに着目しただけだから、
実際の逆伝播はもう少し複雑になるだろうな・・・。

以前も説明したと思うが、
単純パーセプトロンの本来の活性化関数はヘヴィサイド関数。
構造としては以下のようになる。
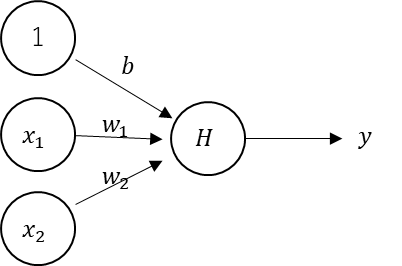

活性化関数がヘヴィサイド関数だと、勾配が無いから、
逆伝播が効かないんだよね。

そうそう。
そこで、活性化関数をシグモイド関数に差し替えたものを
今回の単純パーセプトロンとしている。
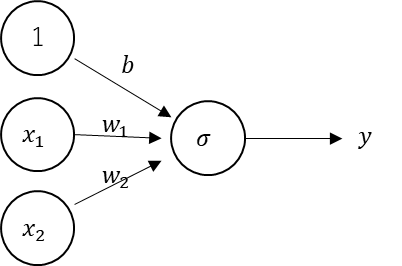

これで逆伝播が効くようになるわけだ。

本来の単純パーセプトロンは逆伝播による学習はしないが、
逆伝播の最もシンプルな挙動をみるには単純パーセプトロンくらいシンプルな構造な方が見やすいので、
無理やり採用してる感じだな。

逆伝播は本来だと誤差逆伝播法が正式名称だけど、
単純パーセプトロンに使用される用語ではないところから、
意図的に「逆伝播」って言い方にしたんだよね。
逆伝播の復習

逆伝播の復習をしておこう。
重みの逆伝播
\(
\begin{eqnarray}
\displaystyle\frac{\partial E}{\partial W}&=&\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}\frac{\partial Z}{\partial W}\\
&=&(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}\cdot X
\end{eqnarray}
\)
バイアスの逆伝播
\(
\begin{eqnarray}
\displaystyle\frac{\partial E}{\partial b}&=&\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}\frac{\partial Z}{\partial b}\\
&=&(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}\cdot 1\\
&=&(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}
\end{eqnarray}
\)

こうしてみると、重みとバイアスの逆伝播って途中まで一緒なんだな。

その着眼点は良いね。
つまり、プログラム化する際に表現の最適化が可能。
次回はその点について掘り下げる。

(なんかやぶ蛇感が・・・。)
まとめ

まとめだよ。
- 単純パーセプトロンの構造について復習。
- 今回扱うのは活性化関数をシグモイド関数に差し替えたもの。
- 逆伝播の復習。
- 重みとバイアスの逆伝播は途中まで一緒。
- よって表現の最適化が可能。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント