バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
単純パーセプトロンに対する逆伝播を行う。
まずは逆伝播を行った際の重みの動き方を確認するプログラムを作成する。
今回はPythonでこれを実現する。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】プログラム化する数式

まずは、今回プログラム化する数式を再掲。
\(
\begin{eqnarray}
\displaystyle\frac{\partial E}{\partial W}&=&(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}\cdot X\\
&=&\sum \Bigg\{\Bigg(\begin{bmatrix}a_1\\a_2\\a_3\\a_4\end{bmatrix}-\begin{bmatrix}0\\0\\0\\1\end{bmatrix}\Bigg)\Bigg\}\circ
\sigma\Bigg(\begin{bmatrix}z_1\\z_2\\z_3\\z_4\end{bmatrix}\Bigg)
\Bigg\{1-\sigma\Bigg(\begin{bmatrix}z_1\\z_2\\z_3\\z_4\end{bmatrix}\Bigg)\Bigg\}
\begin{bmatrix}1&1\end{bmatrix}
\begin{bmatrix}0&0\\0&1\\1&0\\1&1\end{bmatrix}
\end{eqnarray}
\)

これをPythonで実現する。
重みはそれぞれ2.7近辺に収束すればOKだ。
Pythonコード

以下がPythonコード。
import numpy as np
import matplotlib.pyplot as plt
# シグモイド関数の定義
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# シグモイド関数の導関数の定義
def sigmoid_derivative(x):
return sigmoid(x) * (1 - sigmoid(x))
# データセットの定義
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
Y = np.array([[0], [0], [0], [1]])
W = np.array([1.0, 6.0])
b = -4.0
N = 200 # ループ回数
aW = np.zeros((N, 2)) # 重み記録用バッファ
for i in range(N):
# 順伝播
Z = X@W.reshape(-1,1) + b
A = sigmoid(Z)
# 逆伝播
dW = np.sum((A - Y) * sigmoid_derivative(Z)@np.ones((1,2)) * X, axis=0)
# パラメータの更新
W = W - dW
aW[i, :] = W # 重みを記憶
plt.plot(aW) # 重みの変化の経緯をplot
plt.legend(['w_1', 'w_2'])
plt.grid(True)
plt.show()
print("W =", W) # 最終的な重み処理結果

処理結果は以下。
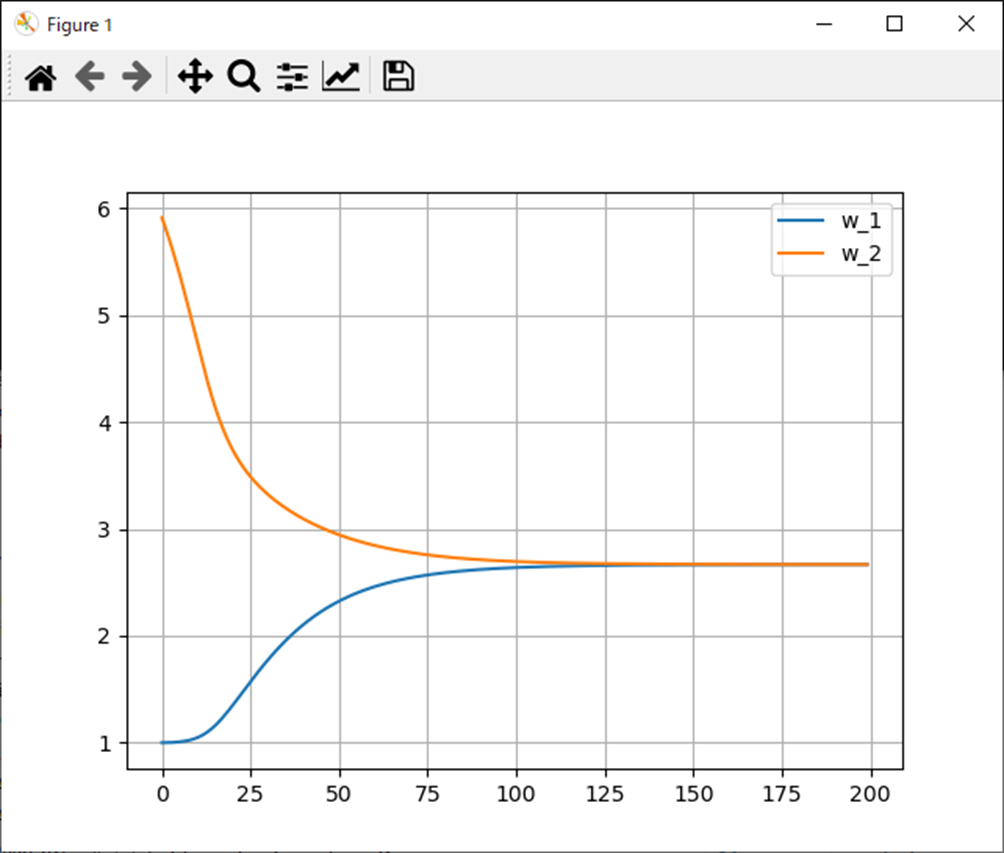
W = [2.66643661 2.66689667]
まとめ

まとめだよ。
- 逆伝播を行った際の重みの動き方を確認するプログラムをPythonで作成。
- おおよそ狙ったところに収束。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント