MATLAB,Python,Scilab,Julia比較 第4章 その58【逆伝播⑨】

バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/

はじめに
登場人物
【再掲】入力、出力パターン
入力パターンが増えると・・・。
まとめ

はじめに

単純パーセプトロンに対する逆伝播についての話。
入力、出力が複数であるが故の連鎖律の事情。

登場人物

博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1

エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1

【再掲】入力、出力パターン

フクさん

まず、今回の単純パーセプトロンに対しての入力、出力のパターンを再掲しておこう。

\(x_1\)	\(x_2\)	\(y\)
0	0	0
0	1	0
1	0	0
1	1	1

太郎くん

確か、ANDゲートの真理値表だよね。

入力パターンが増えると・・・。

フクさん

入力パターンが増えると、連鎖律の考え方も少し変わる。
ひとつづつ学習するオンライン学習の場合は加味不要だが、
バッチ学習、ミニバッチ学習のように、ある程度の入力と出力(ラベル)のデータセットを一括で実施する場合、
連鎖律のルートが増えることになる。

太郎くん

そういえば、以前そんなこと言ってたな・・・。

フクさん

図で書くとこんな感じになる。

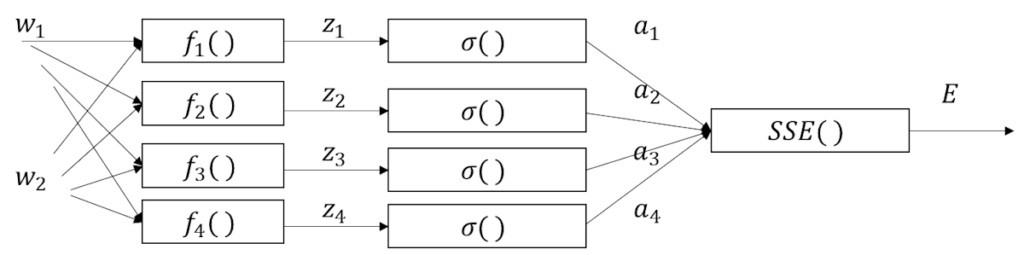
データセットを加味した場合の連鎖律(重み)、w1、w2、f1()、f2()、f3()、f4()、z1、z2、z3、z4、σ()、a1、a2、a3、a4、SSE()、E

フクさん

そして、数式で書くとこんな感じ。

\(
\displaystyle\frac{\partial E}{\partial w_1}=
\frac{\partial E}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial w_1}
+\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial w_1}
+\frac{\partial E}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial w_1}
+\frac{\partial E}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial w_1}
\)

\(
\displaystyle\frac{\partial E}{\partial w_2}=
\frac{\partial E}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial w_2}
+\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial w_2}
+\frac{\partial E}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial w_2}
+\frac{\partial E}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial w_2}
\)

太郎くん

なんだこの地獄は・・・。

フクさん

ちなみにバイアスも似たような感じ。

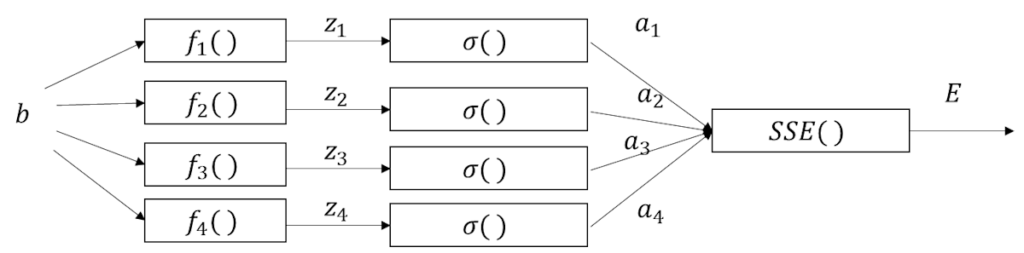
データセットを加味した場合の連鎖律(バイアス)、b、f1()、f2()、f3()、f4()、z1、z2、z3、z4、σ()、a1、a2、a3、a4、SSE()、E

\(
\displaystyle\frac{\partial E}{\partial b}=
\frac{\partial E}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial b}
+\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial b}
+\frac{\partial E}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial b}
+\frac{\partial E}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial b}
\)

太郎くん

大魔境じゃねぇか・・・。

フクさん

実際にプログラム化する際は、こういった点に注意が必要ってことだな。