バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
単純パーセプトロンに対する逆伝播についての話。
誤差関数の微分について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】逆伝播を想定した単純パーセプトロンの構成

まずは、逆伝播を想定した単純パーセプトロンの構成を再掲。


今回は、誤差関数の微分について。
誤差関数の位置づけ

逆伝播を行う上で、連鎖律を解くわけだが、
基本的にはブロック図上の後ろから解いていく。
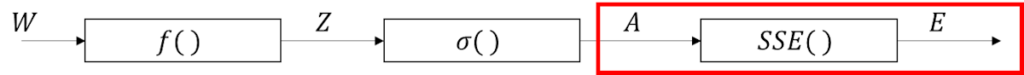

前からじゃないのか。

まぁ、別にどこからでも良いんだけどね。
ちなみに連鎖律で見ると前からになる。
\(
\displaystyle\frac{\partial E}{\partial W}={\color{red}\frac{\partial E}{\partial A}}\frac{\partial A}{\partial Z}\frac{\partial Z}{\partial W}
\)

そうすると、誤差関数からやる方が自然って感じになるのか。
誤差関数

誤差関数は二乗和誤差を1/2にした、ちょい変形したものを使用する。
これは以前説明したように、微分した際にシンプルな式になるため。
\(
\displaystyle E={\color{red}\frac{1}{2}}\sum_{i=1}^n(\hat{y}_i-y_i)^2
\)

確かにそういうこと言ってたね。
誤差関数の偏導関数

これにAとYを代入したものが以下
\(
\displaystyle E=\frac{1}{2}\sum_{i=1}^n(A-Y)^2=\frac{1}{2}\sum_{i=1}^n(A^2-2AY+Y^2)
\)

これの偏導関数が以下になる。
\(
\displaystyle \frac{\partial E}{\partial A}=\frac{1}{2}\sum_{i=1}^n(2A-2Y)=\frac{1}{2}\sum_{i=1}^n(A-Y)
\)

イヤーな感じの数式だと思ってたけど、
やってみたらそれほど複雑ではないんだね。
まとめ

まとめだよ。
- 連鎖律に於ける誤差関数の位置づけを確認。
- ブロック図的には一番後ろだが、連鎖律としては先頭。
- 誤差関数の確認。
- 誤差関数の偏導関数の確認。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント