バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
勾配降下法をプログラム的に確認する方法をもう少し掘り下げた話。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】勾配降下法の確認プログラムのフロー

とりあえず、勾配降下法の確認プログラムのフローを再掲
- 目的関数の定義
- 目的関数の導関数の定義
- 入力初期値設定
- ハイパーパラメータの設定
- 勾配降下法の実装
- 結果表示
- グラフへのプロット

「入力初期値設定」「ハイパーパラメータの設定」「グラフへのプロット」について掘り下げる
入力初期値設定

まずは、入力初期値設定だが、
これは単純に2.9にしておこう。
前回みせたグラフをベースにするとこの位置を入力初期値とする。
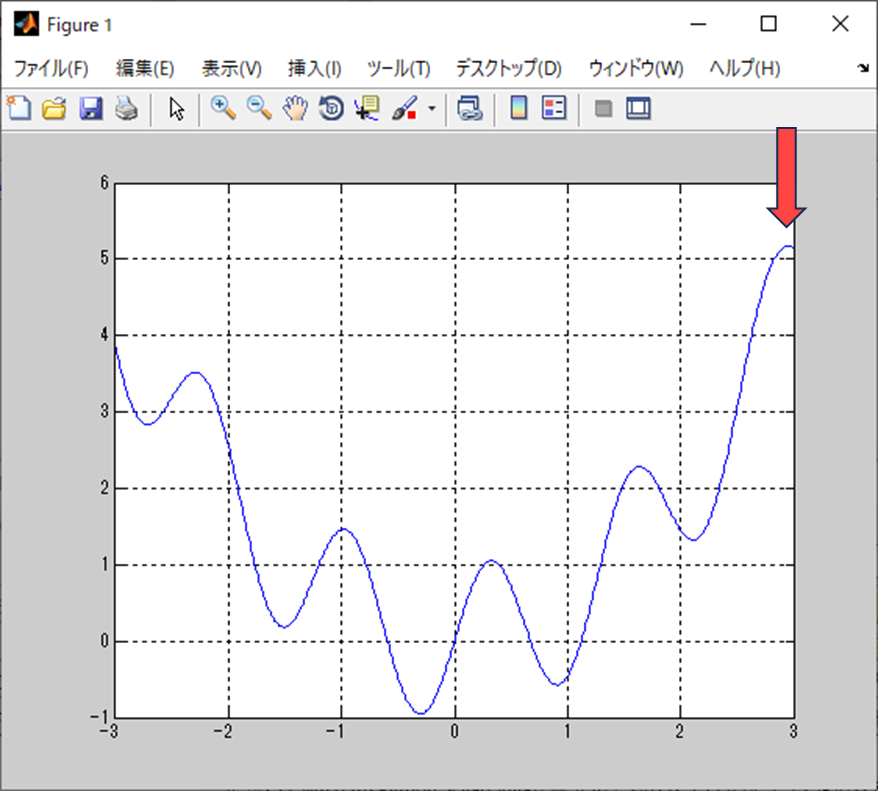

なるほど。
上の方から下っていく感じを想定するのか。
確かに名前のとおり勾配を降下していく感じがしそう。
ハイパーパラメータの設定

次はパイパーパラメータ。

そもそもパイパーパラメータがわからん。

モデルが学習する上での設定値だと思えばOKだ。
最適化アルゴリズム毎に変わるところではあるな。

じゃー、とりあえずは今回のハイパーパラメータがどんなのかを見て察するか。

今回に於けるハイパーパラメータは以下
- 学習率
- 勾配大きさに対して重みを変動させる係数
- 最大イテレーション数
- 勾配降下法の実行回数

なるほど。
確かに学習時の設定値だ。
グラフへのプロット

グラフへのプロットだが、
学習の経緯も見れた方が良い。
というわけで、学習過程の入力の軌跡や誤差の動きを記録する。
まぁ、勾配降下法を実施する際にfor分で回すことになるから、
それぞれの変数を配列として保存して、あとでグラフで表示するって感じだな。
具体的な実装は、これから作るソースコードを見てもらった方が良いだろう。

じゃー、とりあえずは今回のハイパーパラメータがどんなのかを見て察するか。
プログラムの振る舞いの雰囲気

で、実際のプログラムの振る舞いを事前に出しておこう。
分かり易いようにアニメーションgifにしてある。
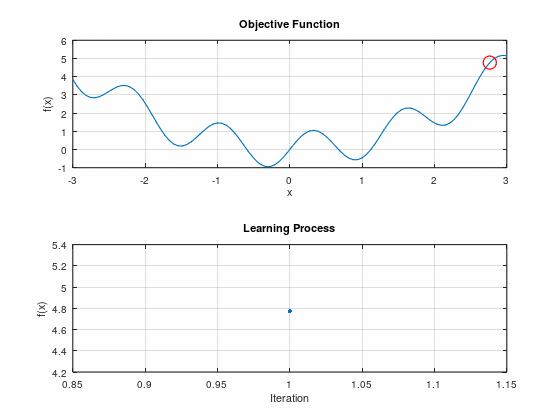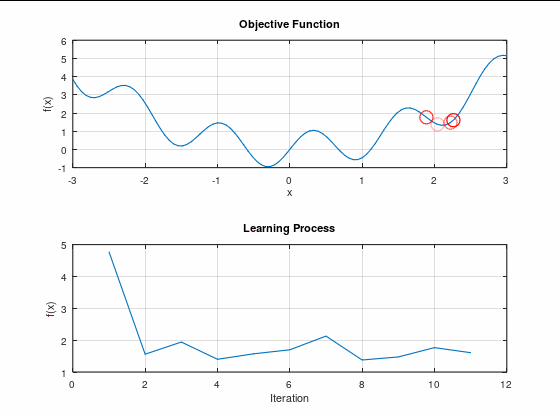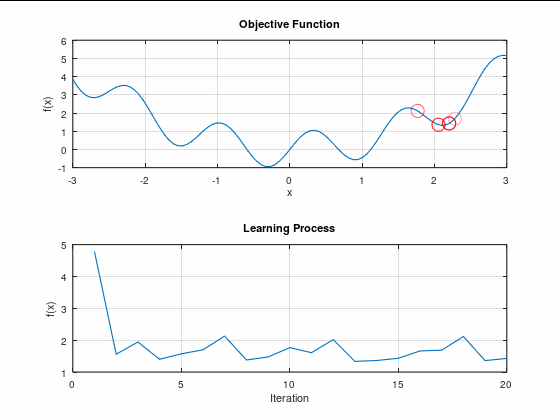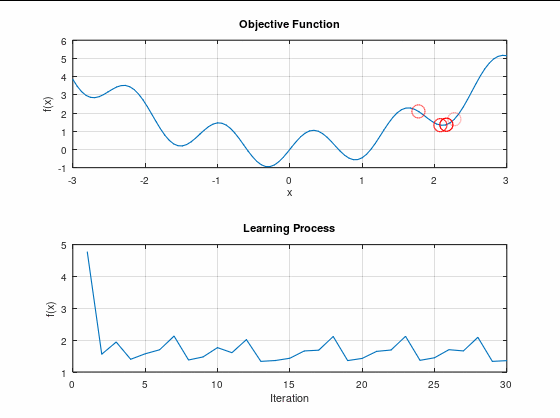

なんかごちゃごちゃ動いとる!

でも、最小値まで行ってないね?

こういう状況を「局所最適解に陥る」と言ったりする。
最適解は共に誤差関数の極小値ではあるのだが、最小値ではない。
最小値ではない極小値が局所最適解。
最小値な極小値が大域最適解。
って呼ばれている。

なるほど。
これが勾配降下法の問題ってやつか。

それ以外にも様々な問題はあるのだが、
直近で我々がぶち当たる問題はこれだな。
まとめ

まとめだよ。
- 勾配降下法プログラムのフローで分かりにくいところを説明。
- 入力初期値は学習のスタート地点。
- ハイパーパラメータは学習アルゴリズムの設定値。
- グラフへのプロットは履歴付きで。
- プログラムの振る舞いをアニメーションgifで確認。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント