バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
勾配降下法をプログラム的に確認する方法の話。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
勾配降下法をプログラム的に確認する方法

前回、勾配降下法の実験をするって言ってけど、
何をするの?

勾配降下法の利用シーンはニューラルネットワークの学習などではあるが、
概念自体は関数の最小値の探索だ。
つまり、適当な関数を定義して、極小値目指して下っていく感じが見れればOK。

その適当な関数とは・・・。

とりあえず、こんな関数かな。
\(
\displaystyle f(x)=\sin(5x)+\frac{x^2}{2}
\)

三角関数と二次関数を合成したものだな。
波形としては以下になる。
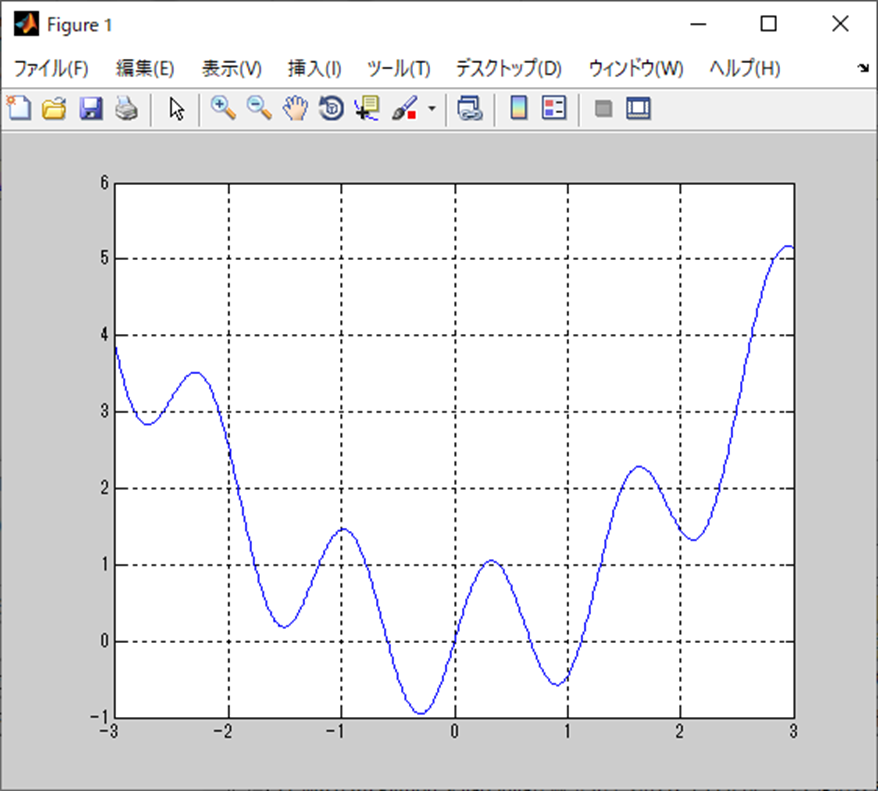

すげぇナミナミしてんなぁ・・・。

傾きを知るためには導関数が必要だ。
先ほどの関数の導関数がこれ。
\(
f(x)=5\sin(5x)+x
\)

三角関数の導関数を求める証明もあるのだが、
今回の本筋ではないので、この証明は省略だ。

(いきなりそんなんツッコまれても困る・・・。)
プログラムの流れ

で、プログラムの流れとしてはどうなるの?

以下の流れだな。
- 目的関数の定義
- 目的関数の導関数の定義
- 入力初期値設定
- ハイパーパラメータの設定
- 勾配降下法の実装
- 結果表示
- グラフへのプロット

まぁまぁやることあるな・・・。

まぁ、「目的関数の定義」と「目的関数の導関数の定義」は
先ほどの関数とその導関数の話だ。
「入力初期値」、「ハイパーパラメータ」は少し説明が必要かもね。
「勾配降下法の実装」以降は上記を利用して実際に処理するところ。
「結果表示」は学習結果。
グラフへのプロットもそのままではあるが、
ある程度の学習過程が分かるようなプロット方法で実装する予定だ。
下の流れだな。

(途中から何言ってるのかわからんかったけど、フクさんが実装してくれるなら別にいいか・・・。)
まとめ

まとめだよ。
- 勾配降下法をプログラム的に確認する方法としてニューラルネットワークではなく、任意の関数に試す方法がある。
- 三角関数と二次関数を合成したもので試す。
- プログラムのフローを記載。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント