バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
再び連鎖律の解説に戻る。
今回からは勾配降下法の話。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】連鎖律を把握するための知識

多変量関数の連鎖律の話が終わったから、
また元の連鎖律を把握するフローに戻ってくる感じだね。
- 逆数の微分公式(済)
- 積の微分公式(済)
- 商の微分公式(済)
- シグモイド関数の導関数(済)
- 多変量関数の連鎖律(済)
- 勾配降下法

これで残りは勾配降下法のみだ。
勾配降下法

まず勾配降下法の概念的な説明だ。
目的変数と単純パーセプトロンの差を誤差\(E\)とし、
重みを\(W\)とする。
この二つのパラメータの関係をグラフにした場合、
以下の図のようなことをしたいのが勾配降下法。
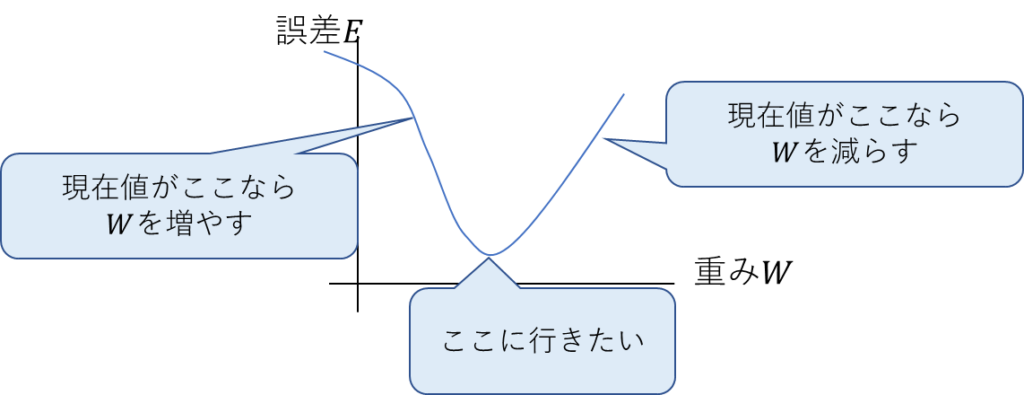

つまり、誤差を最小化したいってことだよね。

でも、どうやって最小値に行くんだ?
値を振って探す感じ?

それだと、総当たり法とかわなくなっちゃうな。

そういうばそうか。
最小値が分かる方法があるってこと?

微分を使う。
微分は関数の傾きがわかる。
要は以下のことをすればOKだ。
- \(\displaystyle \frac{dE}{dW}\)がマイナス(負の勾配)の場合は\(W\)を増やす。
- \(\displaystyle \frac{dE}{dW}\)がプラス(正の勾配)の場合は\(W\)を減らす。

なるほど。
微分すれば良いのか。

って、どう微分するんだ?
単純パーセプトロンでも結構複雑そうだぞ・・・。

それを実現するために、前回までに「多変量関数の連鎖律」をやったわけだ

そうか。
「多変量関数の連鎖律」が分かるってことは単純パーセプトロン全体の導関数が分かるってことだから、
あらゆる点に於ける微分もわかるってことか。
厄介なシグモイド関数も導関数が分かってるし。

そこらへんの一連の流れを誤差逆伝播法と言ったりするな。
まぁ、実際は多層パーセプトロン以上のモデルで使う用語ではあるので、
単純パーセプトロンで使用する場合は、逆伝播という言い方に留めておこう。

名前は聞いたことあるぞ。
何を試すのか

で、その逆伝播ってのを早速試してみる感じになるのかな?

そうしたいのだが、
その前に勾配降下法のみの実験をやってみるつもりだ。
勾配降下法ならではの問題もあるしね。

(毎度のことながら不穏だな・・・。)
まとめ

まとめだよ。
- 勾配降下法に概念レベルの説明。
- 連鎖律含めた一連の流れを誤差逆伝播法と言う。
- ただし、単純パーセプトロンの段階では逆伝播という言葉にしておく。
- まずは勾配降下法のみの実験をやってみる。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント