バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
多変量関数の連鎖律の解説。
今回は多変数関数の連鎖律を元にニューラルネットワークを意識した場合の話。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】多変量関数の連鎖律を把握するための知識

とりあえず多変量関数の連鎖律を把握するための知識を再掲。
- 合成関数(済)
- 合成関数の微分(連鎖律)(済)
- 多変数関数の連鎖律
- 学習データの多入力による暗黙的関数追加

今回は多変数関数の連鎖律を元にニューラルネットワークを意識した場合の話になる。
ニューラルネットワーク的な感じで関数構成を書き直す

多変量関数の連鎖律をニューラルネットワークで想定した場合に少し厄介な話が前回あったけど?

まずは、想定関数構成を見せよう。
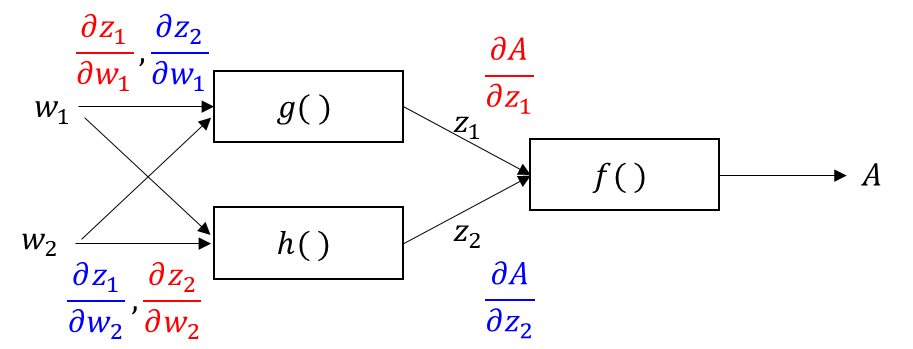

前回の図に似てはいるけど、入力がそれぞれの関数に入ってる感じが違う点かな?

そうだね。
よって、連鎖律の経路が少し複雑になる。
加えて、ニューラルネットワークの場合、動かしたい値は入力ではなく、重みの方。
よって、重みが連鎖律に於ける入力になる。

言いたいことはわかるけど、確かに少し難解になったな・・・。

と言っても基本的な考え方は変わらない。
ニューラルネットワーク的な感じで関数構成の連鎖律を数式で

先ほどの関数構成を元に連鎖律を書き出すと以下になる。
\(
\begin{eqnarray}
\displaystyle \frac{A}{w_1}=\frac{A}{z_1}\frac{z_1}{w_1}+\frac{A}{z_2}\frac{z_2}{w_1}\\
\displaystyle \frac{A}{w_2}=\frac{A}{z_1}\frac{z_1}{w_2}+\frac{A}{z_2}\frac{z_2}{w_2}\\
\end{eqnarray}
\)

\(w_1,w_2\)ともに\(z_1,z_2\)の経路を通るので、
それぞれの経路の連鎖律を合成すればOKだ。

合計するだけでいいの?

うん。
それぞれの変化が求まるから、変化の合計がトータルの変化だから。

なるほど。そういう考え方か。

これがニューラルネットワークを想定した場合の多変量関数の連鎖律になる。
まとめ

まとめだよ。
- ニューラルネットワークを想定した場合の多変量関数の連鎖律について説明。
- 入力から見た際の関数の伝達ルートが複数になる。
- 変化させたいのは入力ではなく重み。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント