MATLAB,Python,Scilab,Julia比較 第4章 その39【多変量関数の連鎖律③】

バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/

はじめに
登場人物
【再掲】多変量関数の連鎖律を把握するための知識
合成関数の微分(連鎖律)の証明
まとめ

はじめに

多変量関数の連鎖律の解説。
今回は合成関数の微分の証明の話。

登場人物

博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1

エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1

【再掲】多変量関数の連鎖律を把握するための知識

太郎くん

とりあえず多変量関数の連鎖律を把握するための知識を再掲。

合成関数(済)
合成関数の微分(連鎖律)
多変数関数の連鎖律
学習データの多入力による暗黙的関数追加

フクさん

今回は合成関数の微分の証明の話になる。
想定される関数は以下。

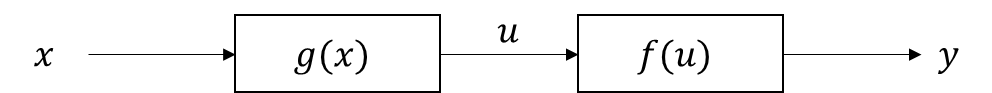
合成関数の微分(連鎖律)の証明

フクさん

では、前回言ったように証明を行っていく。

太郎くん

お手柔らかにお願いするよー。

フクさん

まず、合成関数の微分した際に以下のルールが適用できる。

\(
\displaystyle{f(g(x))}^\prime=\frac{dy}{du}\frac{du}{dx}
\)

太郎くん

前回言ってたやつだね。

フクさん

これを証明していく。

\(
\begin{eqnarray}
\displaystyle{f(g(x))}^\prime&=&\lim_{h\to0}\frac{f(g(x+h))-f(g(x))}{h}\\
\displaystyle&=&\lim_{h\to0}\frac{f(g(x+h))-f(g(x))}{\color{red}g(x+h-g(x))}\frac{\color{red}g(x+h-g(x))}{h}\dots(分母分子にg(x+h)-g(x))\\
\displaystyle&=&\lim_{h\to0}\frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x))}\cdot g^\prime(x)
\end{eqnarray}
\)

太郎くん

またトリッキーなことしてるなー。

太郎くん

2番目と最後の式の変形がよくわからんな。

フクさん

それは以下が成立するからだな。

\(
\displaystyle g^\prime(x)=\lim_{h\to0}\frac{g(x+h)-g(x)}{h}
\)

太郎くん

なるほど。
それを代入したってことか。

フクさん

そして、
\(g(x+h)-g(x)=j\)
とし、\(h\to0\)のとき、\(j\to0\)なので
先ほどの式は以下に変形できる。

\(
\begin{eqnarray}
g(x+h)&=&g(x)-j\\
\displaystyle \{f(g(x))\}^\prime&=&\lim_{j\to0}\frac{f(g(x+j))-f(g(x))}{j}\cdot g^\prime(x)\\
&=&f^\prime(g(x))g^\prime(x)
\end{eqnarray}
\)

太郎くん

なんかすげぇ変形がされたな・・・。

フクさん

ここまでくれば後一歩。

\(
\begin{eqnarray}
u&=&g(x)\\
\displaystyle \{f(g(x))\}^\prime&=&f^\prime(g(x))g^\prime(x)\\
\displaystyle &=&\frac{dy}{dx} =f^\prime(u)g^\prime(x)=\frac{dy}{du}\frac{du}{dx}\\
\displaystyle \frac{dy}{dx}&=&\frac{dy}{du}\frac{du}{dx}//
\end{eqnarray}
\)