バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
シグモイド関数の導関数とオイラー法で求めた微分を比較するプログラムを作成する。
今回はPython(NumPy)。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】シグモイド関数、シグモイド関数の導関数、シグモイド関数のオイラー法での微分の式

まずは、シグモイド関数、シグモイド関数の導関数、シグモイド関数のオイラー法での微分の式を再掲。
シグモイド関数
\(
\displaystyle\sigma(x)=\frac{1}{1+e^{-x}}
\)
シグモイド関数の導関数
\(
\sigma\prime(x)=\sigma(x)\{1-\sigma(x)\}
\)
シグモイド関数のオイラー法による微分
\(
\displaystyle\sigma\prime_{euler}(x)=\frac{\sigma(x+h)-\sigma(x)}{h}\dots h=0.01
\)

これをPythonでplotして比較してみる。
導関数とオイラー法を比較して同一ならOK。
Pythonコード

Pythonコードは以下。
import numpy as np
import matplotlib.pyplot as plt
# シグモイド関数の定義
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# シグモイド関数の導関数の定義
def sigmoid_derivative(x):
return sigmoid(x) * (1 - sigmoid(x))
# オイラー法で微分する関数の定義
def euler_derivative(x, h):
return (sigmoid(x + h) - sigmoid(x)) / h
# x軸の値の範囲と間隔の設定
x = np.arange(-10, 10, 0.1)
# シグモイド関数の計算
y_sigmoid = sigmoid(x)
y_derivative = sigmoid_derivative(x)
# オイラー法で微分した結果の計算
h = 0.01 # ステップサイズ
y_euler_derivative = euler_derivative(x, h)
# グラフを上下に並べて表示
plt.figure()
plt.subplot(3, 1, 1)
plt.plot(x, y_sigmoid)
plt.title('Sigmoid Function')
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.grid(True)
plt.subplot(3, 1, 2)
plt.plot(x, y_derivative)
plt.title('Derivative of Sigmoid Function')
plt.xlabel('x')
plt.ylabel("sigmoid'(x)")
plt.grid(True)
plt.subplot(3, 1, 3)
plt.plot(x, y_euler_derivative)
plt.title('Derivative of Sigmoid Function using Euler Method')
plt.xlabel('x')
plt.ylabel("sigmoid'(x)")
plt.grid(True)
plt.tight_layout() # グラフ間のスペースを調整
plt.show()
処理結果

処理結果は以下。
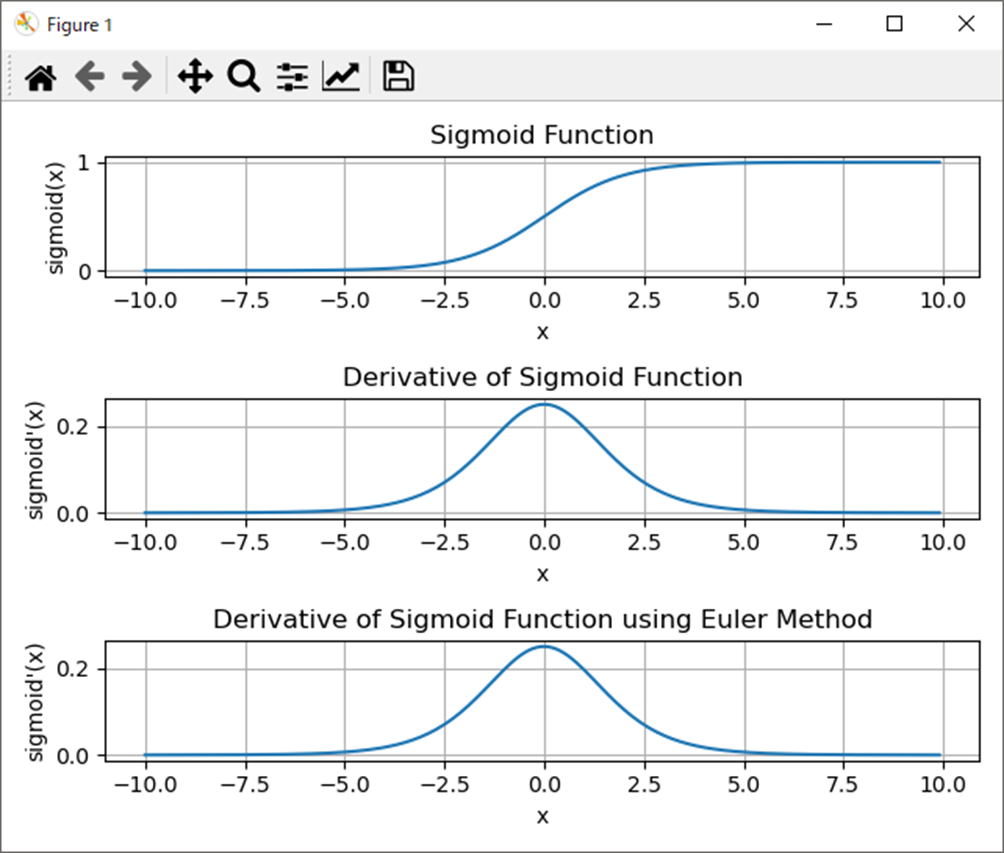

よって、
導出した導関数は正しいと言える。
まとめ

まとめだよ。
- シグモイド関数、シグモイド関数の導関数、シグモイド関数のオイラー法での微分をPythonで算出。
- グラフで比較し、導出した導関数は正しいと言える結果となった。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント