バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
シグモイド関数についての説明。
カスタムヘヴィサイド関数(造語)とシグモイド関数の比較についても。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
決定境界直線の一般的な安定化方法

今回はシグモイド関数を説明してくれるんだよね。

そうそう。
まずはWikipediaから引用。
シグモイド関数(シグモイドかんすう、英: sigmoid function)は、次の式
\(
\displaystyle\varsigma=\frac{1}{1+e^{-ax}}=\frac{tanh(ax/2)+1}{2}
\)で表される実関数である。ここで、 \(a\)をゲイン (gain) と呼ぶ。 シグモイド関数は、生物の神経細胞が持つ性質をモデル化したものとして用いられる。
Wikipediaより(https://ja.wikipedia.org/wiki/%E3%82%B7%E3%82%B0%E3%83%A2%E3%82%A4%E3%83%89%E9%96%A2%E6%95%B0)

ようわからん式が・・・。

数式自体は、そういうものなんだなって程度で覚えておけばOKだ。
とくに理屈のようなものはない。
理屈はないが、特性は利用するってスタンスだな。

その特性が0,1を表現可能で、全域で勾配があるってやつか。

そうそう。
あとは、導関数が存在するというのも重要な性質だが、
これについてはいずれ話そう。

あと、「生物の神経細胞場持つ性質」ってあるのがニューラルネットワークっぽい。

細かい経緯はわからないが、ニューラルネットワークのために生まれた関数なのかもね。
カスタムヘヴィサイドとシグモイドの違い

ここまでの説明でカスタムヘヴィサイドとシグモイドの差は分かったとは思うが一応図示しておこう。
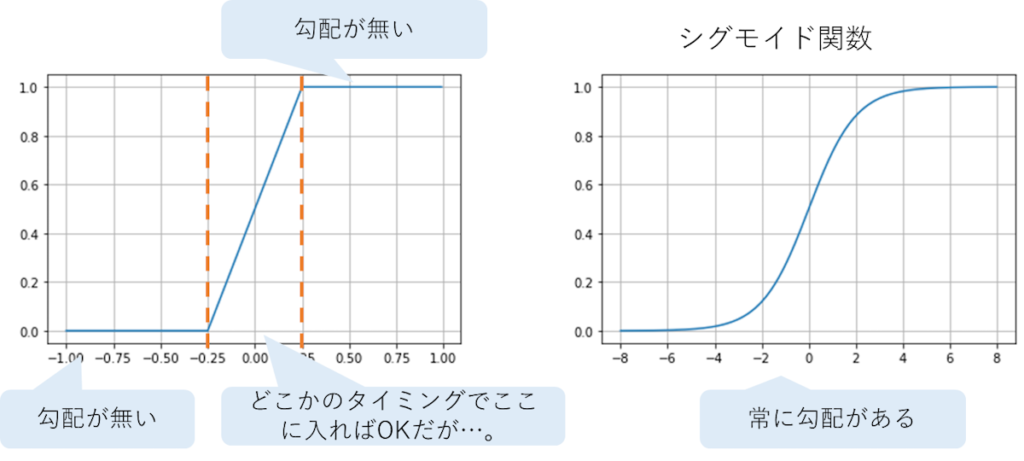

まぁ予想通りな感じだ。
カスタムヘビサイドは±2.5より外側には勾配が無いけど、
シグモイドは常に勾配がある感じ。

今使用している総当たり法の場合、どちらを使用しても同じ結果になるはずだが、
今後予定している誤差逆伝播法を使用し始めるとシグモイドじゃないとかなり都合が悪い。
誤差逆伝播法についても必要になったら説明しよう。

ようわからんが、誤差逆伝播法は全域で勾配が無いと都合が悪いってことか。
プログラム化について

一応カスタムヘヴィサイドの代わりにシグモイドを使用したプログラムを作成するが、
本当に関数を差し替えるだけだ。
よって、ソースコードは作成するが細かい考察はしない予定だ。

まぁ、総当たり法ではカスタムヘヴィサイドとシグモイドに効能的な差がなさそうだから
それでもよさそう。
まとめ

まとめだよ。
- シグモイド関数の定義について説明。
- 特に理屈はなく、そういうものが存在するって程度。
- カスタムヘヴィサイドとシグモイドの比較。
- 総当たり法では効能の差は出ないが、誤差逆伝播法を使い始めるとシグモイドじゃないと都合が悪い。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント