バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
形式ニューロンの決定境界直線がギリギリのところにある問題の対策としてカスタムヘヴィサイド(造語)を使用したプログラムを作成。
今回はScilab。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】カスタムヘヴィサイド(造語)

まずは、カスタムヘヴィサイド関数の再掲。
\(
\begin{cases}
y=0&(x\le -2.5) \\
y=1&(2.5\le x) \\
y=2x+0.5&(-2.5\lt x \lt 2.5)
\end{cases}
\)

今回はこれを活性化関数とした形式ニューロンをScilabで実現する。
Scilabコード

Scilabコードは以下。
function output = custom_heaviside(x)
output = (x < -0.25) .* 0 + (x >= -0.25 & x <= 0.25) .* ( 2*x + 0.5 ) + (x > 0.25) .* 1;
endfunction
function NeuronalBruteForceCustomLearningHeaviside()
// データセットの入力
X = [0 0; 0 1; 1 0; 1 1];
// データセットの出力
Y = [0; 0; 0; 1];
// パラメータの初期値
W = zeros(2, 1); // 重み
b = 0; // バイアス
num_epochs = 10000; // 学習のエポック数
learning_rate = 0.1; // 学習率
min_loss = %inf;
learning_range = 4;
n = length(Y);
// 重みの総当たり計算
best_w1 = 0;
best_w2 = 0;
best_b = 0;
for w1 = -learning_range:learning_rate:learning_range
for w2 = -learning_range:learning_rate:learning_range
for b = -learning_range:learning_rate:learning_range
// フォワードプロパゲーション
Z = X * [w1; w2] + b; // 重みとバイアスを使用して予測値を計算
A = custom_heaviside(Z); // ヘヴィサイド活性化関数を適用
// 損失の計算
loss = 1/n * sum((A - Y).^2); // 平均二乗誤差
// 最小損失の更新
if loss < min_loss
min_loss = loss;
best_w1 = w1;
best_w2 = w2;
best_b = b;
end
end
end
// ログの表示
printf('loss: %f\n', min_loss);
printf('weight: w1 = %f, w2 = %f\n', best_w1, best_w2);
printf('bias: b = %f\n', best_b);
end
// 最小コストの重みを更新
W = [best_w1; best_w2];
b = best_b;
// 学習結果の表示
printf('learning completed\n');
printf('weight: w1 = %f, w2 = %f\n', W(1), W(2));
printf('bias: b = %f\n', b);
// 出力結果確認
printf('X=');
disp(X);
printf('Y=');
disp(custom_heaviside(X*[W(1);W(2)]+b));
// 分類境界線のプロット
x1 = linspace(-0.5, 1.5, 100); // x1の値の範囲
x2 = -(W(1) * x1 + b) / W(2); // x2の計算
clf;
scatter(X(Y == 0, 1), X(Y == 0, 2), 'fill','markerFaceColor','r','markerEdgeColor','r');
scatter(X(Y == 1, 1), X(Y == 1, 2), 'fill','markerFaceColor','b','markerEdgeColor','b');
plot(x1, x2, 'k', 'LineWidth', 2);
p=gca();
p.data_bounds(:,1)=[-0.5;1.5];
p.data_bounds(:,2)=[-0.5;1.5];
title('Decision Boundary');
xlabel('x1');
ylabel('x2');
legend('Class 0', 'Class 1', 'Decision Boundary');
xgrid;
endfunction
NeuronalBruteForceCustomLearningHeaviside()処理結果

処理結果は以下。
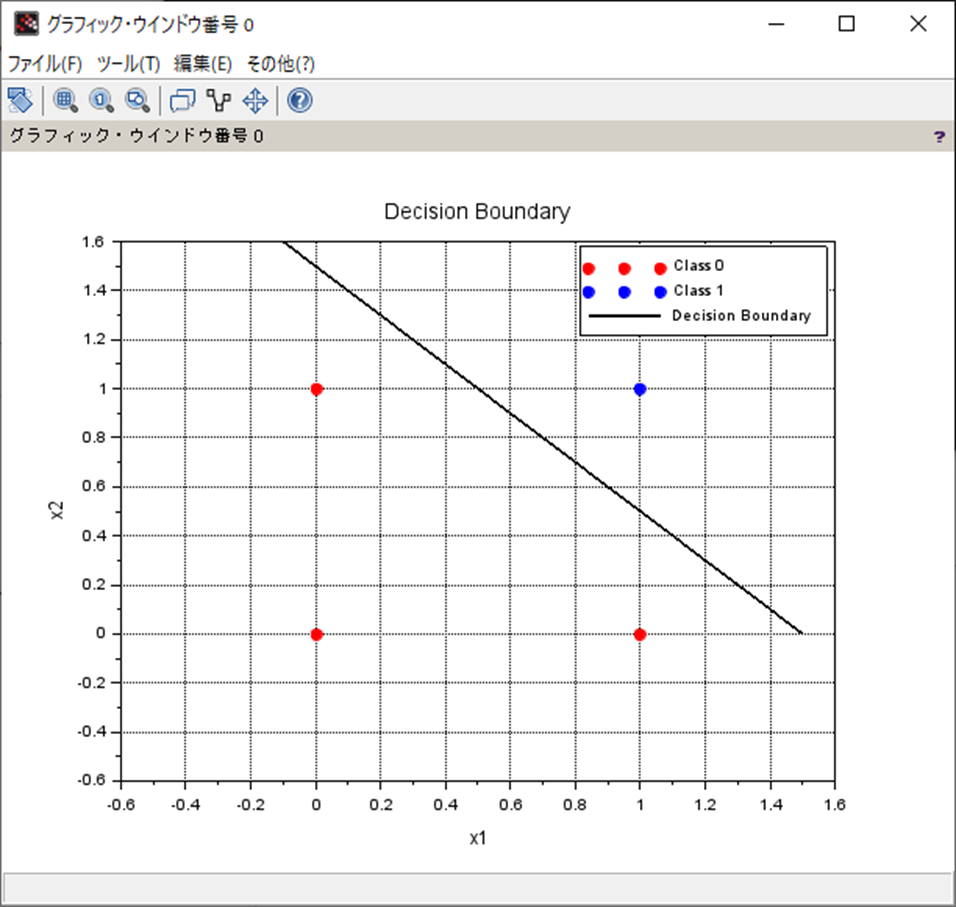
weight: w1 = 0.600000, w2 = 0.600000
bias: b = -0.900000
X=
0. 0.
0. 1.
1. 0.
1. 1.
Y=
0.
0.
0.
1.考察

まぁ、MATLABと一緒だね。

差分は恒例のグラフ表示のところだな。
まとめ

まとめだよ。
- 形式ニューロンの活性化関数をカスタムヘヴィサイド(造語)関数にしたものをScilabで作成。
- おおよそMATLABと同じコード。
- 毎度おなじみのグラフ表示部分に差が出る。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
OpenCVによる画像処理入門
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント