バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
形式ニューロン且つ総当たり法によるパラメータ特定のプログラム化
今回はScilabで実現。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】処理フロー

太郎くん
まずは処理フローを再掲。
- 入力データセットの定義
- 出力データセットの定義
- パラメータ変数の定義(重み、バイアス)
- 学習率定義
- 重みとバイアスの総当たり計算(ループ)
- 重みとバイアスを使用して予測値を算出
- 損失の計算
- 損失の更新
- 最も損失が小さいパラメータの記憶
- 学習結果の表示
- 出力結果の確認

フクさん
これをScilabで実現する。
Scilabコード

フクさん
Scilabコードは以下。
function y = heaviside(x)
y = double(x >= 0);
endfunction
function NeuronalBruteForceLearningHeaviside()
// データセットの入力
X = [0 0; 0 1; 1 0; 1 1];
// データセットの出力
Y = [0; 0; 0; 1];
// パラメータの初期値
W = zeros(2, 1); // 重み
b = 0; // バイアス
num_epochs = 10000; // 学習のエポック数
learning_rate = 0.1; // 学習率
min_loss = %inf;
learning_range = 4;
n = length(Y);
// 重みの総当たり計算
best_w1 = 0;
best_w2 = 0;
best_b = 0;
for w1 = -learning_range:learning_rate:learning_range
for w2 = -learning_range:learning_rate:learning_range
for b = -learning_range:learning_rate:learning_range
// フォワードプロパゲーション
Z = X * [w1; w2] + b; // 重みとバイアスを使用して予測値を計算
A = heaviside(Z); // ヘヴィサイド活性化関数を適用
// 損失の計算
loss = 1/n * sum((A - Y).^2); // 平均二乗誤差
// 最小損失の更新
if loss < min_loss
min_loss = loss;
best_w1 = w1;
best_w2 = w2;
best_b = b;
end
end
end
// ログの表示
printf('loss: %f\n', min_loss);
printf('weight: w1 = %f, w2 = %f\n', best_w1, best_w2);
printf('bias: b = %f\n', best_b);
end
// 最小コストの重みを更新
W = [best_w1; best_w2];
b = best_b;
// 学習結果の表示
printf('learning completed\n');
printf('weight: w1 = %f, w2 = %f\n', W(1), W(2));
printf('bias: b = %f\n', b);
// 出力結果確認
result = heaviside(X*[W(1);W(2)]+b);
printf('X=');disp(X);
printf('hatY=');disp(result);
// 分類境界線のプロット
x1 = linspace(-0.5, 1.5, 100); // x1の値の範囲
x2 = -(W(1) * x1 + b) / W(2); // x2の計算
clf;
scatter(X(Y == 0, 1), X(Y == 0, 2), 'fill','markerFaceColor','r','markerEdgeColor','r');
scatter(X(Y == 1, 1), X(Y == 1, 2), 'fill','markerFaceColor','b','markerEdgeColor','b');
plot(x1, x2, 'k', 'LineWidth', 2);
p=gca();
p.data_bounds(:,1)=[-0.5;1.5];
p.data_bounds(:,2)=[-0.5;1.5];
title('Decision Boundary');
xlabel('x1');
ylabel('x2');
legend('Class 0', 'Class 1', 'Decision Boundary');
xgrid;
endfunction
NeuronalBruteForceLearningHeaviside()処理結果

フクさん
処理結果は以下。
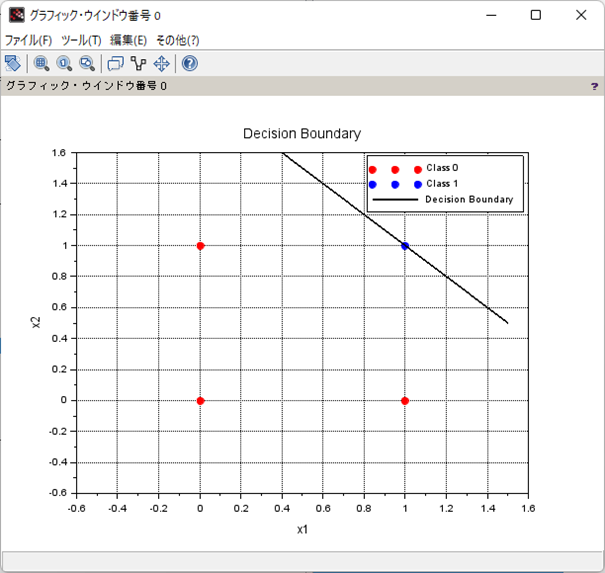
weight: w1 = 0.100000, w2 = 0.100000
bias: b = -0.200000
X=
0. 0.
0. 1.
1. 0.
1. 1.
hatY=
0.
0.
0.
1.
考察

太郎くん
これはMATLABと一緒か。

フクさん
ほぼコピペだな。

太郎くん
決定境界の問題も一緒ってことか・・・。

フクさん
まぁ、その問題は想定内だし、対策もあるから。

太郎くん
それを期待するか。
まとめ

フクさん
まとめだよ。
- 形式ニューロンをScilabで実現。
- ANDの真理値表と同じ結果が得らえれた。
- そして、決定境界線はギリギリな感じはMATLABのときと一緒。
バックナンバーはこちら。




コメント