バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
Adamに至るまでの最適化アルゴリズムの系譜とそれらの依存関係とプログラムで実現する準備まで完了。
これを今回Pythonで実現する。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
Adamの更新式【再掲】

まずはAdamの更新式を再掲。
\(
\begin{eqnarray}
m_{t+1}&=&\beta_1 m_{t-1}+(1-\beta_1)\nabla J(\theta_t)\\
v_{t+1}&=&\beta_2 v_{t-1}+(1-\beta_2)(\nabla J(\theta_t))^2\\
\displaystyle\hat{m}_{t+1}&=&\frac{m_{t+1}}{1-\beta_1}\\
\displaystyle\hat{v}_{t+1}&=&\frac{v_{t+1}}{1-\beta_2}\\
\displaystyle\theta_{t+1}&=&\theta_t-\frac{\alpha}{\sqrt{\hat{v}_{t+1}}+\epsilon}\\
m_t&:&1次のモーメント\\
v_t&:&2次のモーメント\\
\hat{m}_t,\hat{v}_t&:&バイアス補正項\\
\beta_1,\beta_2&:&指数移動平均係数(\beta_1=0.9,\beta_2=0.999)
\end{eqnarray}
\)

これを今回はPythonで実現する。
Pythonコード

Pythonコードは以下。
import numpy as np
import matplotlib.pyplot as plt
# シグモイド関数の定義
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# シグモイド関数の導関数の定義
def sigmoid_derivative(x):
return sigmoid(x) * (1 - sigmoid(x))
# データの準備
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # 入力データ
y = np.array([[0], [1], [1], [0]]) # 出力データ
# ネットワークの構築
hidden_size = 4 # 隠れ層のユニット数
output_size = 1 # 出力層のユニット数
learning_rate = 0.001 # 学習率
input_size = X.shape[1]
W1 = np.random.randn(input_size, hidden_size) # 入力層から隠れ層への重み行列
b1 = np.random.randn(1, hidden_size) # 隠れ層のバイアス項
W2 = np.random.randn(hidden_size, output_size) # 隠れ層から出力層への重み行列
b2 = np.random.randn(1, output_size) # 出力層のバイアス項
# Adamのハイパーパラメータの設定
beta1 = 0.9 # モーメンタムの指数減衰率
beta2 = 0.999 # 2次モーメントの指数減衰率
epsilon = 1e-8 # 数値安定性のための小さな値
# Adam用の変数の初期化
mW1 = np.zeros_like(W1)
mb1 = np.zeros_like(b1)
mW2 = np.zeros_like(W2)
mb2 = np.zeros_like(b2)
vW1 = np.zeros_like(W1)
vb1 = np.zeros_like(b1)
vW2 = np.zeros_like(W2)
vb2 = np.zeros_like(b2)
# 学習
epochs = 20000 # エポック数
errors = np.zeros(epochs) # エポックごとの誤差を保存する配列
for epoch in range(epochs):
# 順伝播
Z1 = np.dot(X, W1) + b1 # 隠れ層の入力
A1 = sigmoid(Z1) # 隠れ層の出力
Z2 = np.dot(A1, W2) + b2 # 出力層の入力
A2 = sigmoid(Z2) # 出力層の出力
# 誤差計算(平均二乗誤差)
error = np.mean((A2 - y) ** 2)
errors[epoch] = error
# 逆伝播
delta2 = (A2 - y) * sigmoid_derivative(Z2)
delta1 = np.dot(delta2, W2.T) * sigmoid_derivative(Z1)
grad_W2 = np.dot(A1.T, delta2)
grad_b2 = np.sum(delta2, axis=0)
grad_W1 = np.dot(X.T, delta1)
grad_b1 = np.sum(delta1, axis=0)
# パラメータの更新
gt_W1 = grad_W1
gt_b1 = grad_b1
gt_W2 = grad_W2
gt_b2 = grad_b2
mW1 = beta1 * mW1 + (1 - beta1) * gt_W1
mb1 = beta1 * mb1 + (1 - beta1) * gt_b1
mW2 = beta1 * mW2 + (1 - beta1) * gt_W2
mb2 = beta1 * mb2 + (1 - beta1) * gt_b2
vW1 = beta2 * vW1 + (1 - beta2) * (gt_W1 ** 2)
vb1 = beta2 * vb1 + (1 - beta2) * (gt_b1 ** 2)
vW2 = beta2 * vW2 + (1 - beta2) * (gt_W2 ** 2)
vb2 = beta2 * vb2 + (1 - beta2) * (gt_b2 ** 2)
mHatW1 = mW1 / (1 - beta1)
mHatb1 = mb1 / (1 - beta1)
mHatW2 = mW2 / (1 - beta1)
mHatb2 = mb2 / (1 - beta1)
vHatW1 = vW1 / (1 - beta2)
vHatb1 = vb1 / (1 - beta2)
vHatW2 = vW2 / (1 - beta2)
vHatb2 = vb2 / (1 - beta2)
W1 -= learning_rate * mHatW1 / (np.sqrt(vHatW1) + epsilon)
b1 -= learning_rate * mHatb1 / (np.sqrt(vHatb1) + epsilon)
W2 -= learning_rate * mHatW2 / (np.sqrt(vHatW2) + epsilon)
b2 -= learning_rate * mHatb2 / (np.sqrt(vHatb2) + epsilon)
# 決定境界線の表示
h = 0.01 # メッシュの間隔
x1, x2 = np.meshgrid(np.arange(np.min(X[:,0])-0.5, np.max(X[:,0])+0.5, h),
np.arange(np.min(X[:,1])-0.5, np.max(X[:,1])+0.5, h))
X_mesh = np.c_[x1.ravel(), x2.ravel()]
hidden_layer_mesh = sigmoid(np.dot(X_mesh, W1) + b1)
output_layer_mesh = sigmoid(np.dot(hidden_layer_mesh, W2) + b2)
y_mesh = np.round(output_layer_mesh) # 出力を0または1に丸める
decision_mesh = y_mesh.reshape(x1.shape) # 分類結果のメッシュを元のグリッドサイズに変形する
colormap = ['#CCFFCC','#FFCCCC'] # 各領域の色を指定する
plt.contourf(x1, x2, decision_mesh, levels=1, colors=colormap) # カラーマップを適用する
plt.scatter(X[y.flatten() == 1, 0], X[y.flatten() == 1, 1], color='r', marker='o', label='Class 1') # クラス1のデータ点を赤でプロット
plt.scatter(X[y.flatten() == 0, 0], X[y.flatten() == 0, 1], color='g', marker='o', label='Class 0') # クラス0のデータ点を緑でプロット
plt.xlabel('X1')
plt.ylabel('X2')
plt.title('XOR Classification')
plt.legend(loc='best')
plt.grid()
plt.show()
plt.plot(errors)
plt.show()処理結果

処理結果は以下となる。
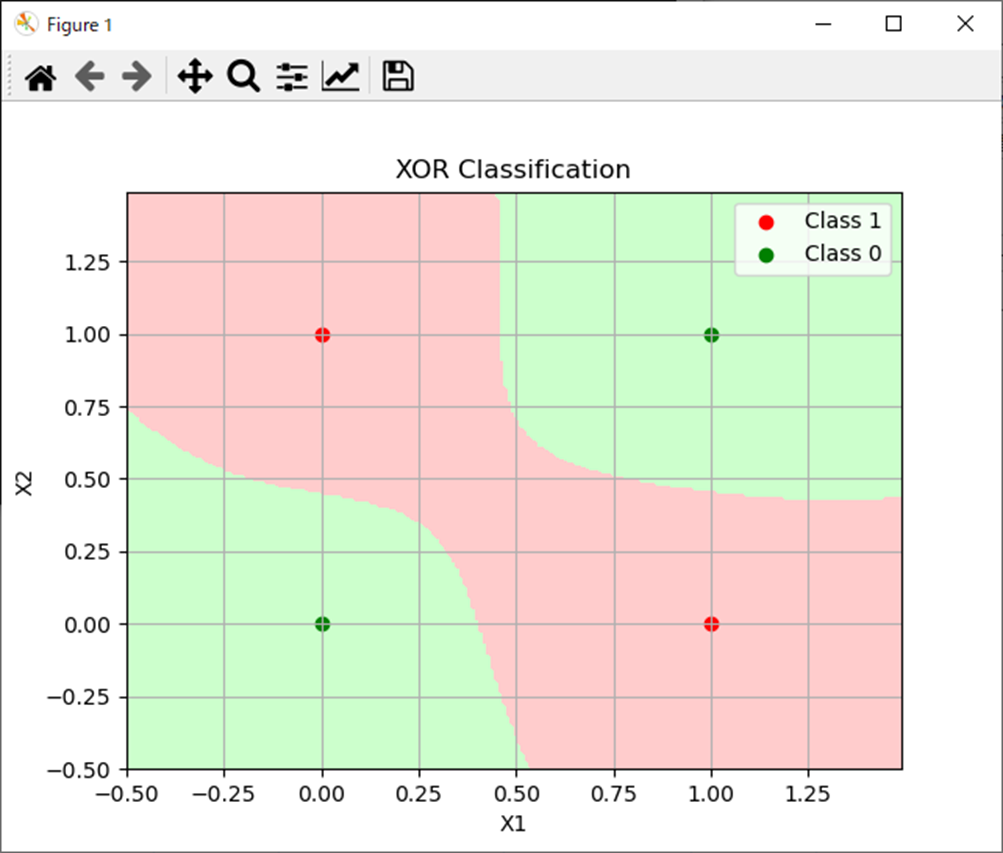
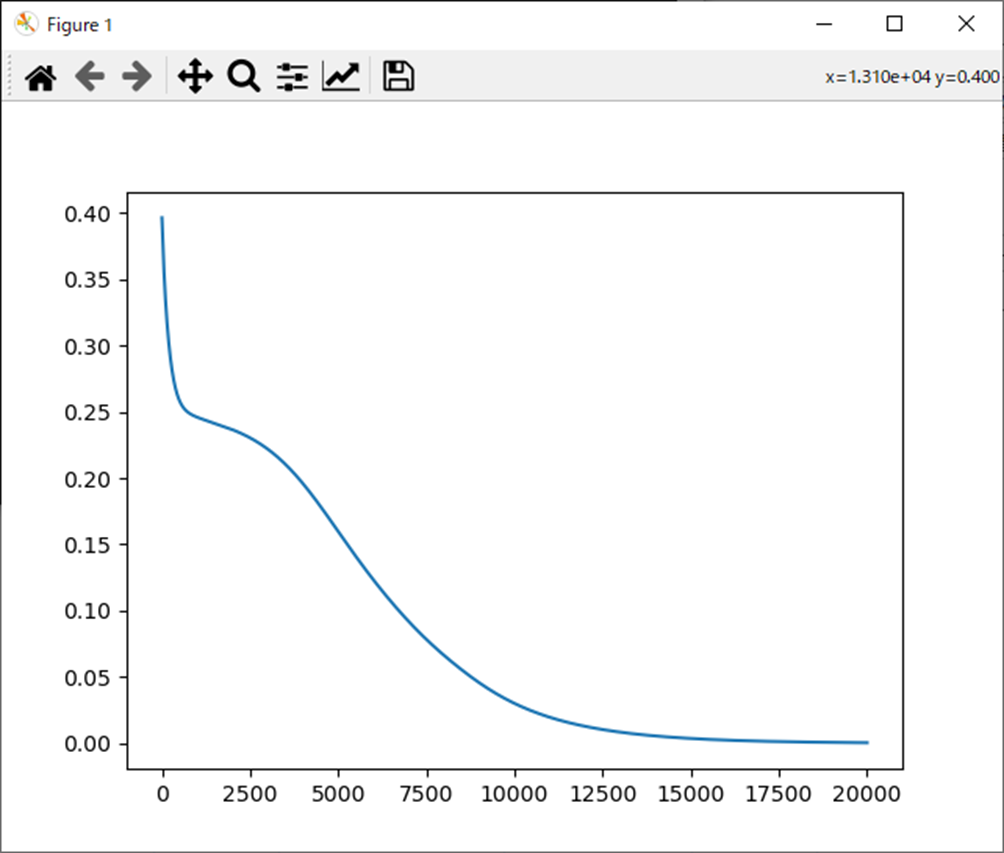
まとめ

まとめだよ。
- ニューラルネットワークの最適化アルゴリズムAdamをPythonにて確認。
- 学習率を0.001にしている都合、収束までは時間がかかる。
- 勾配降下法、モーメンタムでは見れなかった分類パターンが拾えた。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント