バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
形式ニューロンについての解説。
今回は決定境界直線の特定方法について説明。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】形式ニューロンへ至る道

まずは、形式ニューロンへ至る道を再掲。
- ヘヴィサイド関数(済)
- 形式ニューロン(済)
- 分類問題のHelloWorld(済)
- 誤差関数(済)
- 決定境界直線(済)
- 決定境界直線の特定方法
- 総当たり法による分類

今回は決定境界直線の特定方法について説明する。
決定境界直線の必要性

前回、決定境界直線の話をしたが、
分類をする上では、決定境界直線そのものはしらなくても分類は実現可能だ。

え?そうなの?
決定境界直線を境に分類されるから必要だと思うのだけど?

決定境界直線を決定づけるのは学習したモデル。
その学習済みの完成したモデルに対して推論を行わせるには
単純に入力を入れればOK。
利用する側が決定境界直線を意識することはない。

ということは、決定境界直線は無視してOKってこと?

利用するだけだったら無視してもOK。

じゃー無視しよう。

しかし、学習結果としてどこに決定境界直線が引かれているかは見えてないと
その境界線が適切かがわからない。
つまり、学習後のモデルの性能を見る上では重要ってことだな。

で、結局、境界線は求める必要はあるの?ないの?

今回に於いては必要と位置づけよう。
どこに境界線を引いたかは作る側からしたら重要だし。

(結局必要になるんだったらそれでよかったのでは・・・。)
決定境界直線の特定方法

再掲になるが、今回、分類を行うモデルは以下になる。
\(
y=H\Bigg(
\begin{bmatrix}
w_1&w_2&b
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
1
\end{bmatrix}
\Bigg)
\)

そして、境界線はヘヴィサイド関数がどのような出力をしたときのものになるだろうか?

境界線だから、ヘヴィサイド関数が0から1、または1から0に変化した時?

まぁ、それも正解ではあるな。
ただし、その情報だと境界線の特定が困難だ。
ヘヴィサイド関数としてはあり得ない出力だが、
0と1の間の0.5の出力した時が境界線上と仮定しよう。
グラフで表現すると以下の感じだ。
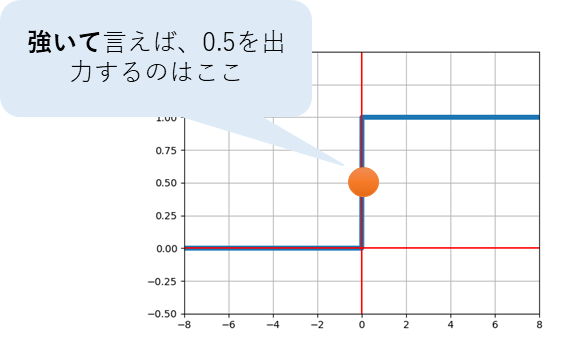

ちょっと理解が追い付いてないけど、
0と1の間を境界線とするってのは納得できるかな。

ヘヴィサイド関数が0.5を出力するのは入力が0の時。
つまり以下の式が成り立つ
\(0.5=H(0)\)

関数の入力と出力の関係で見れば正しいのか。

ヘヴィサイド関数の入力が0の時に決定境界直線上にあると言えるので、以下の式を解いていく。
\(
\begin{eqnarray}
0&=&
\begin{bmatrix}
w_1&w_2&b
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
1
\end{bmatrix}\\
0&=&w_1x_1+w_2x_2+b\\
w_1x_1&=&-w_2x_2-b\\
x_2&=&-\frac{w_1x_1+b}{w_2}
\end{eqnarray}
\)

よって、
\(w_1,w_2,b\)が求まった後であれば、
\(x_1\)から\(x_2\)が求まる。
ここでの\(x_2\)は\(y=0.5\)を満たす決定境界直線を示すものとなる。

(全然わかんねぇけど、数式で求まることがわかってるんだったら大丈夫か・・・。)
まとめ

まとめだよ。
- 決定境界直線の必要性について。
- 推論するだけだったら不要だが、学習済みモデルの性能を評価する際は必要。
- 決定境界直線の特定方法を説明。
- ヘヴィサイド関数の出力が0.5であることを仮定して数式を解けばOK。
バックナンバーはこちら。




コメント